题目内容
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.(Ⅰ)求证:A1D∥平面BCC1B1;
(Ⅱ)求直线CC1与平面DA1C1所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)连接B1C,证明四边形A1B1CD是平行四边形,可得A1D∥B1C,即可证明A1D∥平面BCC1B1;
(Ⅱ)由等体积求出C到平面DA1C1的距离,即可求直线CC1与平面DA1C1所成角的正弦值.
(Ⅱ)由等体积求出C到平面DA1C1的距离,即可求直线CC1与平面DA1C1所成角的正弦值.
解答:
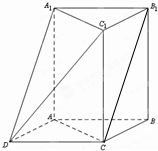 (Ⅰ)证明:连接B1C,则
(Ⅰ)证明:连接B1C,则
∵DC∥A1B1,
∴四边形A1B1CD是平行四边形,
∴A1D∥B1C,
∵A1D?平面BCC1B1,B1C?平面BCC1B1,
∴A1D∥平面BCC1B1;
(Ⅱ)解:△DA1C1中,A1D=C1D=
,A1C1=1,
∴S△DA1C1=
设C到平面DA1C1的距离为h,则由等体积可得
•
•1•1•2=
•
•h,
∴h=
,
∴直线CC1与平面DA1C1所成角的正弦值为
=
.
 (Ⅰ)证明:连接B1C,则
(Ⅰ)证明:连接B1C,则∵DC∥A1B1,
∴四边形A1B1CD是平行四边形,
∴A1D∥B1C,
∵A1D?平面BCC1B1,B1C?平面BCC1B1,
∴A1D∥平面BCC1B1;
(Ⅱ)解:△DA1C1中,A1D=C1D=
| 5 |
∴S△DA1C1=
| ||
| 2 |
设C到平面DA1C1的距离为h,则由等体积可得
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
∴h=
| 2 | ||
|
∴直线CC1与平面DA1C1所成角的正弦值为
| h |
| 2 |
| ||
| 15 |
点评:本题考查线面平行,考查线面角,考查学生分析解决问题的能力,正确求出C到平面DA1C1的距离是关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.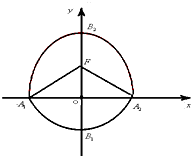 如图,曲线C由半椭圆
如图,曲线C由半椭圆