题目内容
 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.(1)求证:PA⊥平面ABCD;
(2)求二面角E-AC-D的余弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)由题意及正方形的特点,利用BC⊥AB,BC⊥PB得到BC⊥平面PAB,进而得到BC⊥PA,在利用CD⊥PA,得到线面垂直;
(2)由题意及图形,利用三垂线定理得到二面角的平面角,并在三角形中解出即可;
(2)由题意及图形,利用三垂线定理得到二面角的平面角,并在三角形中解出即可;
解答:
 证明:(Ⅰ)∵底面ABCD为正方形,
证明:(Ⅰ)∵底面ABCD为正方形,
∴BC⊥AB,
又∵BC⊥PB,AB∩PB=B,AB,PB?平面PAB,
∴BC⊥平面PAB,
又∵PA?平面PAB,
∴BC⊥PA.
同理CD⊥PA,
又∵BC∩CD=C,BC,CD?平面ABCD,
∴PA⊥平面ABCD.
(2)设M为AD中点,连接EM,
又E为PD中点,
可得EM∥PA,从而EM⊥底面ABCD.
过M作AC的垂线MN,垂足为N,连接EN.
由三垂线定理有EN⊥AC,
∴∠ENM为二面角E-AC-D的平面角.
在Rt△EMN中,可求得EM=
PA=1,MN=
AM=
AD=
,
∴EN=
=
,
∴cos∠ENM=
=
.
∴二面角E-AC-D的余弦值为
.
 证明:(Ⅰ)∵底面ABCD为正方形,
证明:(Ⅰ)∵底面ABCD为正方形,∴BC⊥AB,
又∵BC⊥PB,AB∩PB=B,AB,PB?平面PAB,
∴BC⊥平面PAB,
又∵PA?平面PAB,
∴BC⊥PA.
同理CD⊥PA,
又∵BC∩CD=C,BC,CD?平面ABCD,
∴PA⊥平面ABCD.
(2)设M为AD中点,连接EM,
又E为PD中点,
可得EM∥PA,从而EM⊥底面ABCD.
过M作AC的垂线MN,垂足为N,连接EN.
由三垂线定理有EN⊥AC,
∴∠ENM为二面角E-AC-D的平面角.
在Rt△EMN中,可求得EM=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
∴EN=
| EM2+MN2 |
| ||
| 2 |
∴cos∠ENM=
| MN |
| EN |
| ||
| 3 |
∴二面角E-AC-D的余弦值为
| ||
| 3 |
点评:此题重点考查了线线垂直,线面垂直的判定与性质;还考查了利用三垂线定理求解出二面角的平面角一常用方法;难度中档.

练习册系列答案
相关题目
若椭圆经过原点,且焦点分别为F1(0,1),F2(0,3)则该椭圆的短轴长为( )
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
 多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=
多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD= 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1. 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE= 已知圆O:x2+y2=4.
已知圆O:x2+y2=4.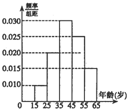 某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示:
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示: