题目内容
在等比数列{an}中,已知a2=2,a3=4,求数列{an}的通项公式及数列的前5项的和S5.
考点:等比数列的前n项和,等比数列的通项公式
专题:等差数列与等比数列
分析:求出数列的首项和公比即可得到结论.
解答:
解:∵在等比数列{an}中,已知a2=2,a3=4,
∴
,解得a1=1,q=2,
则数列{an}的通项公式an=2n-1,数列的前5项的和S5=
=25-1=31.
∴
|
则数列{an}的通项公式an=2n-1,数列的前5项的和S5=
| 1-25 |
| 1-2 |
点评:本题主要考查等比数列的通项公式以及数列前n项的计算,求出数列的首项和公比是解决本题的关键.

练习册系列答案
相关题目
已知函数f(x)的导函数为f′(x),且满足关系式f(x)=x2+3xf′(2)+lnx,则f(1)的值等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知直线l的方程为3x-y+3=0,则l在y轴上的截距为( )
| A、-3 | B、3 | C、-5 | D、5 |
sin
的值为( )
| 37π |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若椭圆经过原点,且焦点分别为F1(0,1),F2(0,3)则该椭圆的短轴长为( )
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
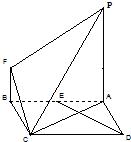 如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF=
如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF= 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.