题目内容
 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.(1)求证:PC⊥AB;
(2)求二面角B-AP-C的大小的余弦.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:空间角,空间向量及应用
分析:(1)利用线面垂直的性质证明PC⊥平面ABC,即可证明PC⊥AB;
(2)建立空间直角坐标系,利用空间向量法即可求二面角B-AP-C的大小的余弦
(2)建立空间直角坐标系,利用空间向量法即可求二面角B-AP-C的大小的余弦
解答:
 解:(1)∵AC=BC=2,AP=BP,∴△APC≌△BPC.
解:(1)∵AC=BC=2,AP=BP,∴△APC≌△BPC.
又PC⊥AC,∴PC⊥BC.
∵AC∩BC=C,
∴PC⊥平面ABC.
∵AB?平面ABC,
∴PC⊥AB.
(2)如图,以C为原点建立空间直角坐标系C-xyz.
则C(0,0,0),A(0,2,0),B(2,0,0).
设P(0,0,t).
∵PB=AB=2
,
∴t=2,P(0,0,2),
取AP中点E,连结BE,CE.
AC=PC,AB=BP,
CE⊥AP,BE⊥AP.
∴∠BEC是二面角B-AP-C的平面角.
∵E(0,1,1),
=(0,-1,-1),
=(2,-1,-1),
∴cos∠BEC=
=
=
.
 解:(1)∵AC=BC=2,AP=BP,∴△APC≌△BPC.
解:(1)∵AC=BC=2,AP=BP,∴△APC≌△BPC.又PC⊥AC,∴PC⊥BC.
∵AC∩BC=C,
∴PC⊥平面ABC.
∵AB?平面ABC,
∴PC⊥AB.
(2)如图,以C为原点建立空间直角坐标系C-xyz.
则C(0,0,0),A(0,2,0),B(2,0,0).
设P(0,0,t).
∵PB=AB=2
| 2 |
∴t=2,P(0,0,2),
取AP中点E,连结BE,CE.
AC=PC,AB=BP,
CE⊥AP,BE⊥AP.
∴∠BEC是二面角B-AP-C的平面角.
∵E(0,1,1),
| EC |
| EB |
∴cos∠BEC=
| ||||
|
|
| 2 | ||||
|
| ||
| 3 |
点评:本题主要考查空间直线和平面垂直的判断,以及空间二面角和距离的计算,利用向量法是解决本题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知直线l的方程为3x-y+3=0,则l在y轴上的截距为( )
| A、-3 | B、3 | C、-5 | D、5 |
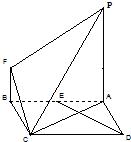 如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF=
如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF= 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.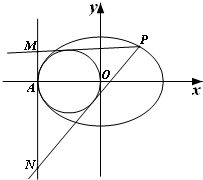 如图,离心率为
如图,离心率为