题目内容
数列{an}的前n项和为Sn,满足an=
,且a1=
.
(Ⅰ)求a2,a3,a4;
(Ⅱ)猜想数列{an}的通项公式,并用数学归纳法加以证明.
| Sn |
| n(2n-1) |
| 1 |
| 3 |
(Ⅰ)求a2,a3,a4;
(Ⅱ)猜想数列{an}的通项公式,并用数学归纳法加以证明.
考点:数学归纳法
专题:综合题,点列、递归数列与数学归纳法
分析:(Ⅰ)利用已知条件通过n=2,3,4,直接计算a2,a3,a4的值,
(Ⅱ)根据(Ⅰ)的计算结果,猜想的通{an}项公式,用数学归纳法的证明步骤直接证明即可.
(Ⅱ)根据(Ⅰ)的计算结果,猜想的通{an}项公式,用数学归纳法的证明步骤直接证明即可.
解答:
解:(Ⅰ)a2=
;a3=
;a4=
…(3分)
(Ⅱ)猜想数列{an}的通项公式为an=
…(6分)
下面用数学归纳法进行证明:
(1)当n=1时,a1=
,猜想成立.…(7分)
(2)假设当n=k时,ak=
成立,…(8分)
则当n=k+1时,由ak+1=
,得Sk+1=(k+1)(2k+1)ak+1,
由ak=
,得Sk=k(2k-1)ak,…(10分)
两式作差得:Sk+1-Sk=(k+1)(2k+1)ak+1-k(2k-1)ak,
即ak+1=
,所以猜想成立.…(13分)
综上所述,对一切正的自然数都有an=
.…(14分)
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 7×9 |
(Ⅱ)猜想数列{an}的通项公式为an=
| 1 |
| (2n-1)(2n+1) |
下面用数学归纳法进行证明:
(1)当n=1时,a1=
| 1 |
| 3 |
(2)假设当n=k时,ak=
| 1 |
| (2k-1)(2k+1) |
则当n=k+1时,由ak+1=
| Sk+1 |
| (k+1)(2k+1) |
由ak=
| Sk |
| k(2k-1) |
两式作差得:Sk+1-Sk=(k+1)(2k+1)ak+1-k(2k-1)ak,
即ak+1=
| 1 |
| (2k+1)(2k+3) |
综上所述,对一切正的自然数都有an=
| 1 |
| (2n-1)(2n+1) |
点评:本题考查数列递推关系式以及通项公式的应用,数学归纳法的证明方法的应用,考查计算能力与逻辑推理能力.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
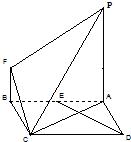 如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF=
如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF= 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1. 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=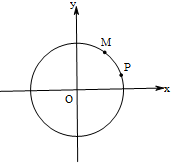 已知圆O:x2+y2=4.
已知圆O:x2+y2=4.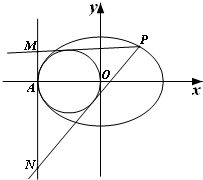 如图,离心率为
如图,离心率为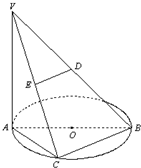 如图,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.
如图,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.