题目内容
求函数f（x）=x4+5x3-27x2-101x-70的零点．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：将函数转化为f（x）=x4+5x3-27x2-101x-70=（x-5）•（x+7）•（x+2）•（x+1），令f（x）=0，解出即可．
解答：
解：∵f（x）=x4+5x3-27x2-101x-70
=（x-5）•（x+7）•（x+2）•（x+1）
∴函数f（x）=x4+5x3-27x2-101x-70的零点是：5、-7、-2、-1．
=（x-5）•（x+7）•（x+2）•（x+1）
∴函数f（x）=x4+5x3-27x2-101x-70的零点是：5、-7、-2、-1．
点评：本题考察了函数的零点问题，进行恰当的因式分解是解题的关键，本题属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1是a2与b2的等比中项，1是
与
的等差中项，则
的值是（ ）
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
A、1或
| ||
B、1或-
| ||
C、1或
| ||
D、1或-
|
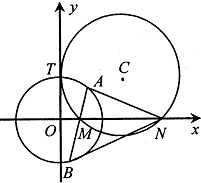圆C与y轴切于点（0，2），与x轴正半轴交于两点M，N（点M在点N的左侧），且|MN|=3．