题目内容
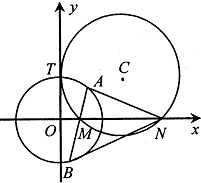 圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.
圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.(1)求圆C的方程;
(2)过点M任作一直线与圆O:x2+y2=4相交于A,B,连接AN,BN,求证:kAN+kBN=0.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设圆的圆心为(a,2),则半径为a,根据|MN|=3,圆心C到弦MN的距离为2,求得r=a=
,从而可以写出圆的标准方程.
(2)设AB:x=ty+1,代入x2+y2-4=0,得:(t2+1)y2+2ty-3=0,由此利用韦达定理结合已知条件能证明kAN+kBN=0.
| 5 |
| 2 |
(2)设AB:x=ty+1,代入x2+y2-4=0,得:(t2+1)y2+2ty-3=0,由此利用韦达定理结合已知条件能证明kAN+kBN=0.
解答:
(1)解:由已知可设C(a,2)(a>0),圆C的半径r=a,
又∵|MN|=3
圆心C到弦MN的距离为2,
故r2=d2+(
)2=4+
=
,
∴a=r=
,(4分)
∴圆C的方程为(x-
)2+(y-2)2=
.
(2)证明:设AB:x=ty+1,代入x2+y2-4=0,
并整理得:(t2+1)y2+2ty-3=0,
设A(x1,y1),B(x2,y2),
,
kAN+kBN=
+
=
+
=
=0.
又∵|MN|=3
圆心C到弦MN的距离为2,
故r2=d2+(
| |MN| |
| 2 |
| 9 |
| 4 |
| 25 |
| 4 |
∴a=r=
| 5 |
| 2 |
∴圆C的方程为(x-
| 5 |
| 2 |
| 25 |
| 4 |
(2)证明:设AB:x=ty+1,代入x2+y2-4=0,
并整理得:(t2+1)y2+2ty-3=0,
设A(x1,y1),B(x2,y2),
|
kAN+kBN=
| y1 |
| x1-4 |
| y2 |
| x2-4 |
=
| y1 |
| ty1-3 |
| y2 |
| ty2-3 |
=
| 2ty1y2-3(y1+y2) |
| (ty1-3)(ty2-3) |
=0.
点评:本题考查圆的方程的求法,考查两直线的斜率和为零的证明,解题时要认真审题,注意点到直线距离的合理运用.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.