题目内容
已知抛物线x2=2py(p>0)上纵坐标为2的点到焦点的距离为3.
(1)求p的值;
(2)若A,B两点在抛物线上,满足
+
=
,其中M(2,2).则抛物线上是否存在异于A,B的点C,使得经过A、B、C三点的圆和抛物线在点C处有相同的切线?若存在,求出点C的坐标;若不存在,说明理由.
(1)求p的值;
(2)若A,B两点在抛物线上,满足
| AM |
| BM |
| 0 |
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用抛物线的定义,即可求p的值;
(2)确定M为AB的中点,设出直线AB的方程代入抛物线方程,利用韦达定理,求出A,B的坐标.假设存在,求出圆心坐标之间的关系,利用抛物线L在点C处切线的切线与NC垂直,即可确定C的坐标.
(2)确定M为AB的中点,设出直线AB的方程代入抛物线方程,利用韦达定理,求出A,B的坐标.假设存在,求出圆心坐标之间的关系,利用抛物线L在点C处切线的切线与NC垂直,即可确定C的坐标.
解答:
解:(1)∵抛物线x2=2py(p>0)上纵坐标为2的点到焦点的距离为3,
∴
+2=3,
∴p=2;
(2)设A,B两点的坐标为A(x1,y1),B(x2,y2),且x1<x2.
∵
+
=
,可得M为AB的中点,即x1+x2=4.
显然直线AB与x轴不垂直,设直线AB的方程为y-2=k(x-2),即y=kx+2-2k,
将y=kx+2-2k代入x2=4y中,得x2-4kx+8(k-1)=0.
∴x1+x2=4k=4,∴k=1,
∴x2-4x=0,
∴A,B的坐标分别为A(0,0),B(4,4).
假设抛物线L:x2=4y上存在点C(t,
)(t≠0且t≠4),使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线.
设圆的圆心坐标为N(a,b),
∵
,∴
,
解得
∵抛物线L在点C处切线的斜率为k=y′|x=t=
,而t≠0,且该切线与NC垂直,
∴
•
=-1,即-2a+bt-2t-
t3=0.
将
代入上式,得t3-2t2-8t=0.
即t(t-4)(t+2)=0.∵t≠0且t≠4,∴t=-2.
故满足题设的点C存在,其坐标为 (-2,1).
∴
| p |
| 2 |
∴p=2;
(2)设A,B两点的坐标为A(x1,y1),B(x2,y2),且x1<x2.
∵
| AM |
| BM |
| 0 |
显然直线AB与x轴不垂直,设直线AB的方程为y-2=k(x-2),即y=kx+2-2k,
将y=kx+2-2k代入x2=4y中,得x2-4kx+8(k-1)=0.
∴x1+x2=4k=4,∴k=1,
∴x2-4x=0,
∴A,B的坐标分别为A(0,0),B(4,4).
假设抛物线L:x2=4y上存在点C(t,
| t2 |
| 4 |
设圆的圆心坐标为N(a,b),
∵
|
|
解得
|
∵抛物线L在点C处切线的斜率为k=y′|x=t=
| t |
| 2 |
∴
b-
| ||
| a-t |
| t |
| 2 |
| 1 |
| 4 |
将
|
即t(t-4)(t+2)=0.∵t≠0且t≠4,∴t=-2.
故满足题设的点C存在,其坐标为 (-2,1).
点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查抛物线的切线,考查学生的综合能力,难度较大.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
观察下列各式:则72=49,73=343,74=2401,…,则72014的末两位数字为( )
| A、01 | B、43 | C、07 | D、49 |
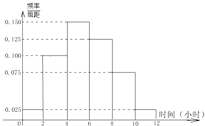 某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)