题目内容
已知函数f(x)=(a+1)lnx+
-x,g(x)=alnx-f(x)+(a-1)x(其中a≥0)
(1)讨论f(x)的单调性;
(2)若g(x)在其定义域内为增函数,求正实数a的取值范围;
(3)设函数h(x)=x(1-x+xg(x)),当a=0时,证明:对?x∈(0,+∞),恒有h(x)<ex-1(1+e-2)成立.
| a |
| x |
(1)讨论f(x)的单调性;
(2)若g(x)在其定义域内为增函数,求正实数a的取值范围;
(3)设函数h(x)=x(1-x+xg(x)),当a=0时,证明:对?x∈(0,+∞),恒有h(x)<ex-1(1+e-2)成立.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求出函数的定义域,导数f′(x),分a=0、0<a<1、a=1、a>1四种情况进行讨论,在定义域内解不等式f′(x)>0,f′(x)<0可得函数的单调区间;
(2)表示出g(x),g(x)在其定义域内为增函数,等价于g′(x)=
≥0对x∈(0,+∞)恒成立,分离出参数a后化为函数的最值即可,利用基本不等式可求函数的最值;
(3)a=0时,要证:h(x)<ex-1(1+e-2)(x>0)成立,即证
<1+e-2成立,即证
<1+e-2成立,可判断x≥1时,
≤0<1+e-2成立.只需证明0<x<1时,
<1+e-2成立,设m(x)=
(0<x<1),利用导数可证0<m(x)<
,从而
<1,于是只证1-x-xlnx<1+e-2,设φ(x)=1-x-xlnx(0<x<1),利用导数可证明;
(2)表示出g(x),g(x)在其定义域内为增函数,等价于g′(x)=
| ax2-x+a |
| x2 |
(3)a=0时,要证:h(x)<ex-1(1+e-2)(x>0)成立,即证
| x(1-x-xlnx) |
| ex-1 |
| ex(1-x-xlnx) |
| ex |
| ex(1-x-xlnx) |
| ex |
| ex(1-x-xlnx) |
| ex |
| x |
| ex |
| 1 |
| e |
| ex |
| ex |
解答:
解:(1)函数的定义域是(0,+∞),
f′(x)=
-
-1=-
=-
(a≥0,x>0),
分类讨论:①当a=0时,函数f(x)在(0,1)上递增,在(1,+∞)上递减;
②当0<a<1时,函数f(x)在(a,1)上递增,在(0,a),(1,+∞)上递减;
③当a=1时,函数f(x)在(0,+∞)上递减;
④当a>1时,函数f(x)在(0,1),(a,+∞)上递减,在(1,a)上递增.
(2)g(x)=-lnx-
+ax(x>0),
∴g′(x)=-
+
+a=
≥0对x∈(0,+∞)恒成立,即ax2-x+a≥0(a>0,x>0)恒成立,
∴a≥
(x>0),设φ(x)=
(x>0),
则a≥φmax(x),而φ(x)=
=
≤
(x=1时取等号),
∴a≥
,即a的取值范围是[
,+∞);
(3)当a=0时,g(x)=-lnx,∴h(x)=x(1-x-xlnx),
要证:h(x)<ex-1(1+e-2)(x>0)成立,即证
<1+e-2成立,即证
<1+e-2成立.
∵当x≥1时,1-x-xlnx≤0,
>0,
∴
≤0<1+e-2成立.
只需证当0<x<1时,
<1+e-2成立,
设m(x)=
(0<x<1),则m′(x)=
=
>0,(0<x<1),
∴m(x)在(0,1)上递增,∴0=m(0)<m(x)<m(1)=
,
∴0<
<1成立,又(1-x)-xlnx>0,
∴
<1-x-xlnx,下面不妨证1-x-xlnx<1+e-2,
设φ(x)=1-x-xlnx(0<x<1),
∵φ′(x)=-1-lnx-1=-2-lnx(0<x<1),
易知φ(x)在(0,e-2)上递增;在(e-2,1)上递减,
φ(x)≤φ(e-2)=1-e-2-e-2lne-2=1+e-2,
综上所述:?x∈(0,+∞),恒有h(x)<ex-1(1+e-2)成立.
f′(x)=
| a+1 |
| x |
| a |
| x2 |
| x2-(a+1)x+a |
| x2 |
| (x-1)(x-a) |
| x2 |
分类讨论:①当a=0时,函数f(x)在(0,1)上递增,在(1,+∞)上递减;
②当0<a<1时,函数f(x)在(a,1)上递增,在(0,a),(1,+∞)上递减;
③当a=1时,函数f(x)在(0,+∞)上递减;
④当a>1时,函数f(x)在(0,1),(a,+∞)上递减,在(1,a)上递增.
(2)g(x)=-lnx-
| a |
| x |
∴g′(x)=-
| 1 |
| x |
| a |
| x2 |
| ax2-x+a |
| x2 |
∴a≥
| x |
| x2+1 |
| x |
| x2+1 |
则a≥φmax(x),而φ(x)=
| x |
| x2+1 |
| 1 | ||
x+
|
| 1 |
| 2 |
∴a≥
| 1 |
| 2 |
| 1 |
| 2 |
(3)当a=0时,g(x)=-lnx,∴h(x)=x(1-x-xlnx),
要证:h(x)<ex-1(1+e-2)(x>0)成立,即证
| x(1-x-xlnx) |
| ex-1 |
| ex(1-x-xlnx) |
| ex |
∵当x≥1时,1-x-xlnx≤0,
| ex |
| ex |
∴
| ex(1-x-xlnx) |
| ex |
只需证当0<x<1时,
| ex(1-x-xlnx) |
| ex |
设m(x)=
| x |
| ex |
| ex-xex |
| e2x |
| 1-x |
| ex |
∴m(x)在(0,1)上递增,∴0=m(0)<m(x)<m(1)=
| 1 |
| e |
∴0<
| ex |
| ex |
∴
| ex(1-x-xlnx) |
| ex |
设φ(x)=1-x-xlnx(0<x<1),
∵φ′(x)=-1-lnx-1=-2-lnx(0<x<1),
易知φ(x)在(0,e-2)上递增;在(e-2,1)上递减,
φ(x)≤φ(e-2)=1-e-2-e-2lne-2=1+e-2,
综上所述:?x∈(0,+∞),恒有h(x)<ex-1(1+e-2)成立.
点评:该题考查利用导数研究函数的单调性、最值及不等式的证明等知识,考查学生的运算求解能力、推理论证能力及转化能力,该题综合性强,难度大,对学生能力要求较高.

练习册系列答案
相关题目
函数y=-xcsx的图象,只可能是下列各图中的( )
A、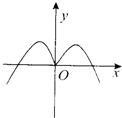 |
B、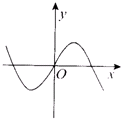 |
C、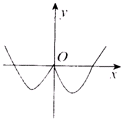 |
D、 |
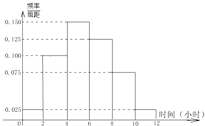 某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时) 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.