题目内容
1是a2与b2的等比中项,1是
与
的等差中项,则
的值是( )
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
A、1或
| ||
B、1或-
| ||
C、1或
| ||
D、1或-
|
考点:等差数列的性质,等比数列的性质
专题:计算题,等差数列与等比数列
分析:先根据1是a2与b2的等比中项,求得ab的值,进而根据
+
=2,求得a+b=2ab,代入
可得答案.
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
解答:
解:∵1是
与
的等差中项,
∴
+
=
=2,即a+b=2ab,
∵1是a2与b2的等比中项,
∴ab=±1,
∴
=
=
=1或-
,
故选:D.
| 1 |
| a |
| 1 |
| b |
∴
| 1 |
| a |
| 1 |
| b |
| a+b |
| ab |
∵1是a2与b2的等比中项,
∴ab=±1,
∴
| a+b |
| a2+b2 |
| a+b |
| (a+b)2-2ab |
| 2ab |
| 4a2b2-2ab |
| 1 |
| 3 |
故选:D.
点评:本题主要考查了等比数列和等差数列的性质.解题的关键是利用等差中项和等比中项求得a和b的关系.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
复数z=
+(a2+2a-3)i(a∈R)为纯虚数,则a的值为( )
| a(a+2) |
| a-1 |
| A、a=0 |
| B、a=0,且a≠-1 |
| C、a=0,或a=-2 |
| D、a≠1,或a≠-3 |
观察下列各式:则72=49,73=343,74=2401,…,则72014的末两位数字为( )
| A、01 | B、43 | C、07 | D、49 |
身高与体重有关系可以用( )分析来分析.
| A、残差 | B、回归 |
| C、二维条形图 | D、独立检验 |
2014°是第( )象限角.
| A、一 | B、二 | C、三 | D、四 |
函数y=-xcsx的图象,只可能是下列各图中的( )
A、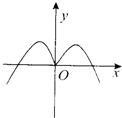 |
B、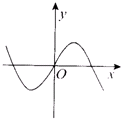 |
C、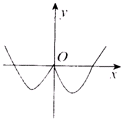 |
D、 |