题目内容
| lim |
| x→0 |
| 1 |
| x2 |
| 1 |
| xsinx |
考点：极限及其运算
专题：函数的性质及应用
分析：多次利用罗比达法则求函数的极限，从而得到结果．
解答：
解：
（
-
）=
=
=
=
=
=
=-
．
| lim |
| x→0 |
| 1 |
| x2 |
| 1 |
| xsinx |
| lim |
| x→0 |
| sinx-x |
| x2sinx |
| lim |
| x→0 |
| cosx-1 |
| 2xsinx+x2cosx |
| lim |
| x→0 |
| -sinx |
| 2sinx+2xcosx+2xcosx-x2sinx |
=
| lim |
| x→0 |
| -cosx |
| 2cosx+4cosx-4xsinx-2xsinx-x2cosx |
| lim |
| x→0 |
| -cosx |
| 6cosx-6xsinx-x2cosx |
| -1 |
| 6-0-0 |
| 1 |
| 6 |
点评：本题主要考查利用罗比达法则求函数的极限，正弦函数、余弦函数的导数，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
复数z=
+（a2+2a-3）i（a∈R）为纯虚数，则a的值为（ ）
| a(a+2) |
| a-1 |
| A、a=0 |
| B、a=0，且a≠-1 |
| C、a=0，或a=-2 |
| D、a≠1，或a≠-3 |
2014°是第（ ）象限角．
| A、一 | B、二 | C、三 | D、四 |
函数y=-xcsx的图象，只可能是下列各图中的（ ）
A、 |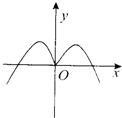
B、 |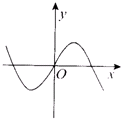
C、 |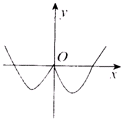
D、 |