题目内容
先阅读下列①、②两个问题,再解决后面的(Ⅰ)、(Ⅱ)两个小题:
①已知a1,a2∈R,且a1+a2=1,求证:a12+22≥
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+a12+a22=2x2-2x+a12+a22,因为对一切x∈R,恒有f(x)≥0,所以△=4-8(a12+a22)≤0,从而得a12+a22≥
.
②同理可证若a1,a2,a3∈R,且a1+a2+a3=1,则a12+a22+a32≥
.
(Ⅰ)若a1,a2,…,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(Ⅱ)参考上述证法,对你推广的结论加以证明.
①已知a1,a2∈R,且a1+a2=1,求证:a12+22≥
| 1 |
| 2 |
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+a12+a22=2x2-2x+a12+a22,因为对一切x∈R,恒有f(x)≥0,所以△=4-8(a12+a22)≤0,从而得a12+a22≥
| 1 |
| 2 |
②同理可证若a1,a2,a3∈R,且a1+a2+a3=1,则a12+a22+a32≥
| 1 |
| 3 |
(Ⅰ)若a1,a2,…,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(Ⅱ)参考上述证法,对你推广的结论加以证明.
考点:函数模型的选择与应用,归纳推理
专题:综合题,函数的性质及应用
分析:(Ⅰ)由已知中已知a1,a2∈R,a1+a2=1,求证a12+a22≥
,及整个式子的证明过程,我们根据归纳推理可以得到一个一般性的公式,若a1,a2,…,an∈R,a1+a2+…+an=1,则a12+a22+…+an2≥
;
(Ⅱ)但此公式是由归纳推理得到的,其正确性还没有得到验证,观察已知中的证明过程,我们可以类比对此公式进行证明.
| 1 |
| 2 |
| 1 |
| n |
(Ⅱ)但此公式是由归纳推理得到的,其正确性还没有得到验证,观察已知中的证明过程,我们可以类比对此公式进行证明.
解答:
解:(Ⅰ)若a1,a2,…,an∈R,a1+a2+…+an=1,求证:a12+a22+…+an2≥
------------------(5分)
(Ⅱ)证明:构造函数
f(x)=(x-a1)2+(x-a2)2+…+(x-an)2
=nx2-2(a1+a2+…+an)x+a12+a22+…+an2
=nx2-2x+a12+a22+…+an2
因为对一切x∈R,都有f(x)≥0,所以△=4-4n(a12+a22+…+an2)≤0
从而证得:a12+a22+…+an2≥
(13分)
| 1 |
| n |
(Ⅱ)证明:构造函数
f(x)=(x-a1)2+(x-a2)2+…+(x-an)2
=nx2-2(a1+a2+…+an)x+a12+a22+…+an2
=nx2-2x+a12+a22+…+an2
因为对一切x∈R,都有f(x)≥0,所以△=4-4n(a12+a22+…+an2)≤0
从而证得:a12+a22+…+an2≥
| 1 |
| n |
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想);(3)对归纳得到的一般性结论进行证明.

练习册系列答案
相关题目
函数y=-xcsx的图象,只可能是下列各图中的( )
A、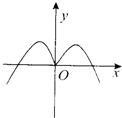 |
B、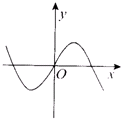 |
C、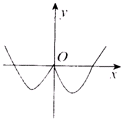 |
D、 |
 边长为2的菱形ABCD中,∠A=60°,沿BD折成直二面角,过点A作PA⊥平面ABC,且AP=2
边长为2的菱形ABCD中,∠A=60°,沿BD折成直二面角,过点A作PA⊥平面ABC,且AP=2 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.四面体B1-BCD的体积是2,求异面直线DB1与CC1所成的角.