题目内容
设正项数列{an}的前n项和为Sn，向量
=（
，1），
=（an+1，2）（n∈N*）满足
∥
．
（1）求数列{an}的通项公式；
（2）设数列{bn}的通项公式为bn=
（t∈N*），若b1，b2，bm（m≥3，m∈N*）成等差数列，求t和m的值；
（3）如果等比数列{cn}满足c1=a1，公比q满足0＜q＜
，且对任意正整数k，ck-（ck+1+ck+2）仍是该数列中的某一项，求公比q的取值范围．
| a |
| Sn |
| b |
| a |
| b |
（1）求数列{an}的通项公式；
（2）设数列{bn}的通项公式为bn=
| an |
| an+t |
（3）如果等比数列{cn}满足c1=a1，公比q满足0＜q＜
| 1 |
| 2 |
考点：数列与向量的综合,等比数列的性质
专题：综合题,等差数列与等比数列
分析：（1）利用
∥
，
=（
，1），
=（an+1，2），可得2
=an+1，即4Sn=（an+1）2，再写一式，两式相减，即可求数列{an}的通项公式；
（2）确定bn=
=
，利用b1，b2，bm（m≥3，m∈N*）成等差数列，建立等式，即可求t和m的值；
（3）先确定ck-（ck+1+ck+2）=qk-1（1-q-q2）是该数列中的某一项，可得1-q-q2是q的几次方形式，从而可求公比q的取值范围．
| a |
| b |
| a |
| Sn |
| b |
| Sn |
（2）确定bn=
| an |
| an+t |
| 2n-1 |
| 2n-1+t |
（3）先确定ck-（ck+1+ck+2）=qk-1（1-q-q2）是该数列中的某一项，可得1-q-q2是q的几次方形式，从而可求公比q的取值范围．
解答：
解：（1）∵
∥
，
=（
，1），
=（an+1，2），
∴2
=an+1，
∴4Sn=（an+1）2，①
n=1时，a1=1；
n≥2时，4Sn-1=（an-1+1）2，②
①-②可得（an+an-1）（an-an-1-2）=0，
∵an＞0，∴an-an-1=2，
∴数列{an}是以1为首项，2为公差的等差数列，
∴an=2n-1；
（2）bn=
=
，
∵b1，b2，bm（m≥3，m∈N*）成等差数列，
∴2×
=
+
，
∴m=3+
，
∵m，t都是正整数，
∴t=2，3，5，m=7，5，4；
（3）cn=qn-1，
∵ck-（ck+1+ck+2）仍是该数列中的某一项，
∴ck-（ck+1+ck+2）=qk-1（1-q-q2）是该数列中的某一项，
∴1-q-q2是q的几次方形式，
∴0＜q＜
，
∴
＜1-q-q2＜1，
∴1-q-q2=q，
∴q=
-1．
| a |
| b |
| a |
| Sn |
| b |
∴2
| Sn |
∴4Sn=（an+1）2，①
n=1时，a1=1；
n≥2时，4Sn-1=（an-1+1）2，②
①-②可得（an+an-1）（an-an-1-2）=0，
∵an＞0，∴an-an-1=2，
∴数列{an}是以1为首项，2为公差的等差数列，
∴an=2n-1；
（2）bn=
| an |
| an+t |
| 2n-1 |
| 2n-1+t |
∵b1，b2，bm（m≥3，m∈N*）成等差数列，
∴2×
| 3 |
| 3+t |
| 1 |
| 1+t |
| 2m-1 |
| 2m-1+t |
∴m=3+
| 4 |
| t-1 |
∵m，t都是正整数，
∴t=2，3，5，m=7，5，4；
（3）cn=qn-1，
∵ck-（ck+1+ck+2）仍是该数列中的某一项，
∴ck-（ck+1+ck+2）=qk-1（1-q-q2）是该数列中的某一项，
∴1-q-q2是q的几次方形式，
∴0＜q＜
| 1 |
| 2 |
∴
| 1 |
| 4 |
∴1-q-q2=q，
∴q=
| 2 |
点评：本题考查数列的通项与求和，考查学生分析解决问题的能力，确定数列的通项是关键．
练习册系列答案
相关题目
2014°是第（ ）象限角．
| A、一 | B、二 | C、三 | D、四 |
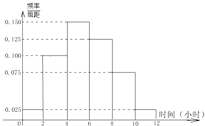某高校共有15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）