题目内容

在△ABC中，内角A，B，C所对的边分别是a，b，c，已知tanA=
sinC
2-cosC
，c=3．
（1）求
b
a
；        
（2）若△ABC的面积为3，求cosC．
考点：正弦定理,余弦定理
专题：三角函数的求值
分析：（1）已知等式利用同角三角函数间的基本关系切化弦，去分母整理后，利用正弦定理化简即可求出所求式子的值；
（2）利用三角形面积公式及余弦定理分别列出关系式，联立即可求出cosC的值．
解答： 解：（1）tanA=
sinA
cosA
=
sinC
2-cosC
，
即2sinA-sinAcosC=cosAsinC，
整理得：2sinA=sinAcosC+cosAsinC=sin（A+C）=sinB，
利用正弦定理
a
sinA
=
b
sinB
化简得：2a=b，
则
b
a
=2；
（2）∵2a=b，△ABC面积为3，c=3，
∴S△ABC=
1
2
absinC=a2sinC=3①，
cosC=
a2+b2-c2
2ab
=
a2+4a2-9
4a2
，即
5
4
-
9
4a2
=cosC②，
联立①②解得：sinC=
3
5
，cosC=
4
5
．
点评：此题考查了正弦、余弦定理，以及三角形面积公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
相关题目
已知a＞0，b＞0，方程为x2+y2-4x+2y=0的曲线关于直线ax-by-1=0对称，则
3a+2b
ab
的最小值为
 
．
若集合A={1，m2}，集合B={3，9}，则“m=3”是“A∩B={9}”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
从[0，10]中任取一个数x，从[0，6]中任取一个数y，则使|x-5|+|y-3|≤4的概率为（　　）
A、
1
2
B、
5
9
C、
2
3
D、
5
12
已知函数f（x）=
2x，x≤1
-f(x-3)，x＞1
，则f（2014）的值为（　　）
A、
1
4
B、2
C、-
1
4
D、-2
某工厂生产A，B两种元件，已知生产A元件的正品率为75%，生产B元件的正品率为80%，生产1个元件A，若是正品则盈利50元，若是次品则亏损10元；生产1个元件B，若是正品则盈利40元，若是次品则亏损5元．
（Ⅰ）求生产5个元件A所得利润不少于140元的概率；
（Ⅱ）设X为生产1个元件A和1个元件B所得总利润，求X的分布列和数学期望．
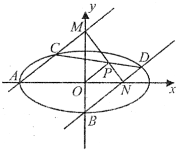如图，过椭圆L的左顶点A（-3，0）和下顶点B且斜率均为k的两直线l1，l2分别交椭圆于C，D，又l1交y轴于M，l2交x轴于N，且CD与MN相交于点P，当k=3时，△ABM是直角三角形．
（Ⅰ）求椭圆L的标准方程；
（Ⅱ）（i）证明：存在实数λ，使得
AM
=λ
OP
；
（ii）求|OP|的取值范围．
下面关于f（x）的判断：
①y=f（x-2）与y=f（2-x）的图象关于直线x=2对称；
②若f（x）为偶函数，且f（2+x）=-f（x），则f（x）的图象关于直线x=2对称．
③设函数f（x）=lnx，且x0，x1，x2∈（0，+∞），若x1＜x2，则
1
x2
＞
f(x1)-f(x2)
x1-x2
．
④函数f（x）=lnx，x0，x1，x2∈（0，+∞），存在x0∈（x1，x2），（x1＜x2），使得
1
x0
=
f(x1)-f(x2)
x1-x2
．
⑤设函数f（x）=x2-3x+4，g(x)=
1
2
x2+4lnx+a．对于?x1∈[1，e]，总?x2∈[1，e]，使得f（x1）=g（x2），则实数a的取值范围为[1，
5
4
]．
其中正确的判断是
 
（把你认为正确的判断都填上）
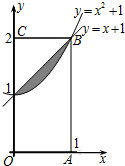如图，在矩形OABC内：记抛物线y=x2+1与直线y=x+1围成的区域为M（图中阴影部分）．随机往矩形OABC内投一点P，则点P落在区域M内的概率是（　　）
A、
1
18
B、
1
12
C、
1
6
D、
1
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网