题目内容
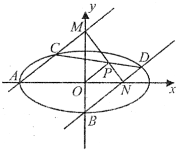如图，过椭圆L的左顶点A（-3，0）和下顶点B且斜率均为k的两直线l1，l2分别交椭圆于C，D，又l1交y轴于M，l2交x轴于N，且CD与MN相交于点P，当k=3时，△ABM是直角三角形．（Ⅰ）求椭圆L的标准方程；
（Ⅱ）（i）证明：存在实数λ，使得
| AM |
| OP |
（ii）求|OP|的取值范围．
考点：椭圆的简单性质
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）根据当k=3时，△ABM是直角三角形，左顶点A（-3，0）和下顶点B，求出b的值，即可求椭圆L的标准方程；
（Ⅱ）（i）设两直线l1，l2的方程分别为y=k（x+3）和y=kx-1，求出C，D的坐标，可得P的坐标，即可得到存在实数λ，使得
=λ
；
（ii）确定P的轨迹方程，可得|OP|的最小值，即可求|OP|的取值范围．
（Ⅱ）（i）设两直线l1，l2的方程分别为y=k（x+3）和y=kx-1，求出C，D的坐标，可得P的坐标，即可得到存在实数λ，使得
| AM |
| OP |
（ii）确定P的轨迹方程，可得|OP|的最小值，即可求|OP|的取值范围．
解答：
（Ⅰ）解：由题意，
∵当k=3时，△ABM是直角三角形，左顶点A（-3，0）和下顶点B
∴
=-
，
∴b=1，
∴椭圆L的标准方程为
+y2=1；
（Ⅱ）（i）证明：设两直线l1，l2的方程分别为y=k（x+3）和y=kx-1，其中k≠0，则M（0，3k），N（
，0）．
y=k（x+3）代入椭圆方程可得（1+9k2）x2+54k2x+81k2-9=0，
方程一根为-3，则由韦达定理可得另一根为
，
∴C（
，
）．
同理D（
，
）
∵两直线l1，l2平行，
∴可设
=t
，
=t
，从而可得P（
，
）
∴
=（
，
）
∵
=（3，3k），
∴存在实数λ=1+3k，使得
=λ
；
（ii）∵
=（
，
），
∴消去参数可得P的轨迹方程为x+3y-3=0，
∴|OP|的最小值为d=
=
∴|OP|的取值范围为[
，+∞）．
∵当k=3时，△ABM是直角三角形，左顶点A（-3，0）和下顶点B
∴
| 0+b |
| -3 |
| 1 |
| 3 |
∴b=1，
∴椭圆L的标准方程为
| x2 |
| 9 |
（Ⅱ）（i）证明：设两直线l1，l2的方程分别为y=k（x+3）和y=kx-1，其中k≠0，则M（0，3k），N（
| 1 |
| k |
y=k（x+3）代入椭圆方程可得（1+9k2）x2+54k2x+81k2-9=0，
方程一根为-3，则由韦达定理可得另一根为
| 3-27k2 |
| 1+9k2 |
∴C（
| 3-27k2 |
| 1+9k2 |
| 6k |
| 1+9k2 |
同理D（
| 18k |
| 1+9k2 |
| 9k2-1 |
| 1+9k2 |
∵两直线l1，l2平行，
∴可设
| MP |
| MN |
| CP |
| CD |
| 3 |
| 1+3k |
| 3k |
| 1+3k |
∴
| OP |
| 3 |
| 1+3k |
| 3k |
| 1+3k |
∵
| AM |
∴存在实数λ=1+3k，使得
| AM |
| OP |
（ii）∵
| OP |
| 3 |
| 1+3k |
| 3k |
| 1+3k |
∴消去参数可得P的轨迹方程为x+3y-3=0，
∴|OP|的最小值为d=
| |-3| | ||
|
3
| ||
| 10 |
∴|OP|的取值范围为[
3
| ||
| 10 |
点评：本题考查椭圆的方程，考查直线与椭圆的位置关系，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目