题目内容
下面关于f(x)的判断:
①y=f(x-2)与y=f(2-x)的图象关于直线x=2对称;
②若f(x)为偶函数,且f(2+x)=-f(x),则f(x)的图象关于直线x=2对称.
③设函数f(x)=lnx,且x0,x1,x2∈(0,+∞),若x1<x2,则
>
.
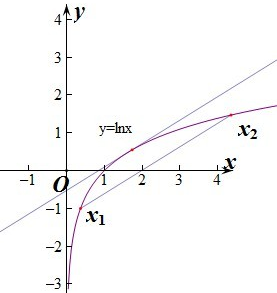
④函数f(x)=lnx,x0,x1,x2∈(0,+∞),存在x0∈(x1,x2),(x1<x2),使得
=
.
⑤设函数f(x)=x2-3x+4,g(x)=
x2+4lnx+a.对于?x1∈[1,e],总?x2∈[1,e],使得f(x1)=g(x2),则实数a的取值范围为[1,
].
其中正确的判断是 (把你认为正确的判断都填上)
①y=f(x-2)与y=f(2-x)的图象关于直线x=2对称;
②若f(x)为偶函数,且f(2+x)=-f(x),则f(x)的图象关于直线x=2对称.
③设函数f(x)=lnx,且x0,x1,x2∈(0,+∞),若x1<x2,则
| 1 |
| x2 |
| f(x1)-f(x2) |
| x1-x2 |
④函数f(x)=lnx,x0,x1,x2∈(0,+∞),存在x0∈(x1,x2),(x1<x2),使得
| 1 |
| x0 |
| f(x1)-f(x2) |
| x1-x2 |
⑤设函数f(x)=x2-3x+4,g(x)=
| 1 |
| 2 |
| 5 |
| 4 |
其中正确的判断是
考点:命题的真假判断与应用
专题:综合题,函数的性质及应用
分析:①令x-2=t,易知y=f(t)与y=f(-t)关于直线t=0对称,从而可判断①的正误;
②利用偶函数的性质,结合①的结论可判断②的正误
③不妨设x1=
,x2=1,代入关系式计算,可判断③之正误;
④利用导数的几何意义,数形结合可判断④的正误;
⑤依题意,可求得当x∈[1,e]时,f(x)∈[
,e2-3e+4],设g(x)=
x2+4lnx+a的值域为M,则[
,e2-3e+4]⊆M,利用函数y=g(x)的单调性解不等式组
可判断⑤.
②利用偶函数的性质,结合①的结论可判断②的正误
③不妨设x1=
| 1 |
| 2 |
④利用导数的几何意义,数形结合可判断④的正误;
⑤依题意,可求得当x∈[1,e]时,f(x)∈[
| 7 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
|
解答:
解:①令x-2=t,则2-x=-t,y=f(t)与y=f(-t)关于直线t=0对称,
∴y=f(x-2)与y=f(2-x)的图象关于直线x=2对称,故①正确;
②∵f(x)为偶函数,f(2+x)=-f(x),
∴f(2-x)=-f(-x)=-f(x)=f(2+x),由①知f(x)的图象关于直线x=2对称,即②正确;
③不妨设x1=
,x2=1,则
=
=2ln2=ln4>1=
,故③错误;
④f′(x)=
,f′(x0)=
,表示在x=x0处的切线的斜率,由图知,过横坐标分别为x1和x2的两点的割线
和过曲线上横坐标为x0的点的切线的斜率可能相等,故④正确;
 ⑤∵f(x)=x2-3x+4=(x-
⑤∵f(x)=x2-3x+4=(x-
)2+
,f(1)=2,f(e)=e2-3e+4,
∴当x∈[1,e]时,f(x)∈[
,e2-3e+4];
∵对于?x1∈[1,e],总?x2∈[1,e],使得f(x1)=g(x2),
设当x∈[1,e]时g(x)=
x2+4lnx+a的值域为M,
则[
,e2-3e+4]⊆M;
又g′(x)=x+
>0,
∴y=g(x)在区间[1,e]上单调递增,
∴
,解得
e2-3e≤a≤
,故⑤错误;
综上所述,①②④正确.
故答案为:①②④.
∴y=f(x-2)与y=f(2-x)的图象关于直线x=2对称,故①正确;
②∵f(x)为偶函数,f(2+x)=-f(x),
∴f(2-x)=-f(-x)=-f(x)=f(2+x),由①知f(x)的图象关于直线x=2对称,即②正确;
③不妨设x1=
| 1 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
ln
| ||
|
| 1 |
| x2 |
④f′(x)=
| 1 |
| x |
| 1 |
| x0 |
和过曲线上横坐标为x0的点的切线的斜率可能相等,故④正确;
 ⑤∵f(x)=x2-3x+4=(x-
⑤∵f(x)=x2-3x+4=(x-| 3 |
| 2 |
| 7 |
| 4 |
∴当x∈[1,e]时,f(x)∈[
| 7 |
| 4 |
∵对于?x1∈[1,e],总?x2∈[1,e],使得f(x1)=g(x2),
设当x∈[1,e]时g(x)=
| 1 |
| 2 |
则[
| 7 |
| 4 |
又g′(x)=x+
| 4 |
| x |
∴y=g(x)在区间[1,e]上单调递增,
∴
|
| 1 |
| 2 |
| 5 |
| 4 |
综上所述,①②④正确.
故答案为:①②④.
点评:本题考查命题的真假判断与应用,着重考查函数的对称性、单调性与值域,着重考查导数的几何意义,考查等价转化思想、构造函数思想、数形结合思想与创新思维,属于难题.

练习册系列答案
相关题目
在△ABC中,
=2
,
=
,
=
,
=
,则下列等式成立的是( )
| AD |
| DC |
| BA |
| a |
| BD |
| b |
| BC |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|