题目内容
已知集合A={x|0<x+3≤9},B={x|b-3<x<b+7},M={x|x2-2x-24≤0且|x|<5},全集U=R.
(1)求A∩M;
(2)若B∪(CUM)=R,求实数b的取值范围.
(1)求A∩M;
(2)若B∪(CUM)=R,求实数b的取值范围.
考点:交、并、补集的混合运算,交集及其运算
专题:集合
分析:(1)求出M中x的范围确定出M,求出A与M的交集即可;
(2)由M及全集U求出M的补集,根据B与M并集为R列出关于b的不等式组,求出不等式组的解集即可确定出b的范围.
(2)由M及全集U求出M的补集,根据B与M并集为R列出关于b的不等式组,求出不等式组的解集即可确定出b的范围.
解答:
解:(1)由A中不等式解得:-3<x≤6,即A={x|-3<x≤6},
由M中的不等式变形得:(x-6)(x+4)≤0,且-5<x<5,
解得:-4≤x<5,即M={x|-4≤x<5},
则A∩M={x|-3<x<5};
(2)∵M={x|-4≤x<5},全集U=R,
∴∁UM={x|x<-4或x≥5},
∵B={x|b-3<x<b+7},且B∪(∁UM)=R,
∴
,
解得:-2≤b<-1,
则实数b的取值范围是[-2,-1).
由M中的不等式变形得:(x-6)(x+4)≤0,且-5<x<5,
解得:-4≤x<5,即M={x|-4≤x<5},
则A∩M={x|-3<x<5};
(2)∵M={x|-4≤x<5},全集U=R,
∴∁UM={x|x<-4或x≥5},
∵B={x|b-3<x<b+7},且B∪(∁UM)=R,
∴
|
解得:-2≤b<-1,
则实数b的取值范围是[-2,-1).
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
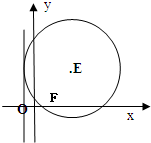 动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C.
动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C. 如图,在△AOB中,点P是AB的中垂线上的一点,|
如图,在△AOB中,点P是AB的中垂线上的一点,| 如图:通过以“直”代“曲”无限逼近的方法求曲边梯形的面积的步骤是
如图:通过以“直”代“曲”无限逼近的方法求曲边梯形的面积的步骤是