题目内容
已知椭圆的中心为原点O,长轴在x轴上,短半轴长为
,离心率e=
,左、右焦点分别为F1、F2.
(Ⅰ)求该椭圆的方程;
(Ⅱ)过F1作直线l交椭圆于P、Q两点(直线l不过原点O),若椭圆上存在点E,使得四边形OPEQ为平行四边形,求直线l的方程.
| ||
| 2 |
| ||
| 5 |
(Ⅰ)求该椭圆的方程;
(Ⅱ)过F1作直线l交椭圆于P、Q两点(直线l不过原点O),若椭圆上存在点E,使得四边形OPEQ为平行四边形,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件得
,由此能求出椭圆的方程.
(Ⅱ) 设x=my-1,设P(x1,y1),Q(x2,y2),E(x0,y0),椭圆上存在点E,使四边形OPEQ为平行四边形,由
,得(6m2+10)y2-12my-9=0,由此能求出直线方程.
|
(Ⅱ) 设x=my-1,设P(x1,y1),Q(x2,y2),E(x0,y0),椭圆上存在点E,使四边形OPEQ为平行四边形,由
|
解答:
解:(Ⅰ)设所求椭圆的标准方程为
+
=1(a>b>0),
∵短半轴长为
,离心率e=
,
∴
,…(3分)
解得a2=
,b2=
,c2=1,
∴所求椭圆的方程为:
+
=1.…(6分)
(Ⅱ) 由(Ⅰ)知F1(-1,0)、F2(1,0),
由题意知直线(x0-a)2+(
-
)2=a2+
的倾斜角不为0,
故不妨设x=my-1…(7分)
设P(x1,y1),Q(x2,y2),E(x0,y0),
椭圆上存在点E,使四边形OPEQ为平行四边形,即
=
+
成立,则
,E(x1+x2,y1+y2),
整理
,得(6m2+10)y2-12my-9=0,
△>0,y1+y2=
,y1•y2=-
①,…(8分)
∵点E在椭圆上,∴
+
=1,
+
+
+
+
+
=1,
又A、B在椭圆上,∴
+
=1,
+
=1.
故12x1x2+20y1y2+15=0②,
x1x2=(my1-1)(my2-1)=m2y1y2-m(y1+y2)+1③,
由①、②、③解得m2=1,m=±1,…(10分)
所求直线方程为:x-y+1=0,x+y+1=0.…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
∵短半轴长为
| ||
| 2 |
| ||
| 5 |
∴
|
解得a2=
| 5 |
| 2 |
| 3 |
| 2 |
∴所求椭圆的方程为:
| 2x2 |
| 5 |
| 2y2 |
| 3 |
(Ⅱ) 由(Ⅰ)知F1(-1,0)、F2(1,0),
由题意知直线(x0-a)2+(
| x02 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
故不妨设x=my-1…(7分)
设P(x1,y1),Q(x2,y2),E(x0,y0),
椭圆上存在点E,使四边形OPEQ为平行四边形,即
| OE |
| OP |
| OQ |
|
整理
|
△>0,y1+y2=
| 12m |
| 6m2+10 |
| 9 |
| 6m2+10 |
∵点E在椭圆上,∴
| 2(x1+x1)2 |
| 5 |
| 2(y1+y1)2 |
| 3 |
| 2x12 |
| 5 |
| 2y12 |
| 3 |
| 2x22 |
| 5 |
| 2y22 |
| 3 |
| 4x1x2 |
| 5 |
| 4y1y2 |
| 3 |
又A、B在椭圆上,∴
| 2x12 |
| 5 |
| 2y12 |
| 3 |
| 2x22 |
| 5 |
| 2y22 |
| 3 |
故12x1x2+20y1y2+15=0②,
x1x2=(my1-1)(my2-1)=m2y1y2-m(y1+y2)+1③,
由①、②、③解得m2=1,m=±1,…(10分)
所求直线方程为:x-y+1=0,x+y+1=0.…(12分)
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
已知A(1,0,3),B(1,2,1),C(0,2,1),三角形ABC的面积为( )
| A、1 | ||
B、
| ||
C、2
| ||
| D、4 |
 (文) 已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.
(文) 已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.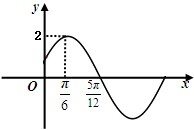 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<