题目内容
已知a、b、c是实数，试比较a2+b2+c2与ab+bc+ca的大小．
考点：不等式比较大小
专题：不等式的解法及应用
分析：从不等式的左边入手，左边对应的代数式的二倍，分别写成两两相加的形式，在三组相加的式子中分别用均值不等式，整理成最简形式，得到右边的2倍，两边同时除以2，得到结果．
解答：
解：∵a2+b2+c2-（ab+bc+ca）=
[（a-b）2+（b-c）2+（c-a）2]≥0，
当且仅当a=b=c时取等号，∴a2+b2+c2≥ab+bc+ca．
| 1 |
| 2 |
当且仅当a=b=c时取等号，∴a2+b2+c2≥ab+bc+ca．
点评：本题考查均值不等式的应用，考查不等式的证明方法，是一个基础题，这种题目常常考虑分拆后利用基本不等式，因为题目分拆后才符合均值不等式的表现形式．
练习册系列答案
相关题目
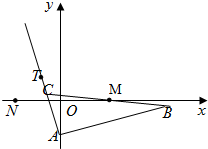已知△ABC的边AB边所在直线的方程为x-3y-6=0，M（2，0）满足BM=MC，点T（-1，1）在AC边所在直线上且满足lAB⊥lAT．