题目内容
已知函数f(x)=(2-a)(x-1)-2lnx,g(x)=ex-x+1.(a为常数,e为自然对数的底,e≈2.71828)
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在区间(0,
)上无零点,求a的最小值.
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在区间(0,
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)a=1时求出导数f′(x),在定义域内解不等式f′(x)>0,f′(x)<0即可;
(Ⅱ)函数f(x)<0在区间(0,
)上不可能恒成立,故要使函数f(x)在区间(0,
)上无零点,只要对?x∈(0,
),f(x)>0恒成立.即对?x∈(0,
),a>2-
恒成立.构造函数,利用导数求出函数的最值即可;
(Ⅱ)函数f(x)<0在区间(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2lnx |
| x-1 |
解答:
解:(Ⅰ)当a=1时,f(x)=x-1-2lnx(x>0),则f′(x)=1-
.
令f′(x)>0得x>2;令f′(x)<0得0<x<2,
故f(x)的单调递减区间为(0,2],单调递增区间为[2,+∞);
(Ⅱ)∵函数f(x)<0在区间(0,
)上不可能恒成立,
故要使函数f(x)在区间(0,
)上无零点,只要对?x∈(0,
),f(x)>0恒成立.即对?x∈(0,
),a>2-
恒成立.
令l(x)=2-
(x∈(0,
),则l′(x)=
=
,
再令m(x)=2lnx+
-2,则m′(x)=
-
=
,
∵x∈(0,
),∴m′(x)<0,
故函数m(x)在区间(0,
)上单调递减,∴m(x)>m(
)=2-2ln2>0,即l′(x)>0,
∴函数l(x)在区间(0,
)上单调递增,∴l(x)<l(
)=2-4ln2,
故只要a≥2-4ln2,函数f(x)在区间(0,
)上无零点,所以amin=2-4ln2.
| 2 |
| x |
令f′(x)>0得x>2;令f′(x)<0得0<x<2,
故f(x)的单调递减区间为(0,2],单调递增区间为[2,+∞);
(Ⅱ)∵函数f(x)<0在区间(0,
| 1 |
| 2 |
故要使函数f(x)在区间(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2lnx |
| x-1 |
令l(x)=2-
| 2lnx |
| x-1 |
| 1 |
| 2 |
-
| ||
| (x-1)2 |
2lnx+
| ||
| (x-1)2 |
再令m(x)=2lnx+
| 2 |
| x |
| 2 |
| x |
| 2 |
| x2 |
| -2(1-x) |
| x2 |
∵x∈(0,
| 1 |
| 2 |
故函数m(x)在区间(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴函数l(x)在区间(0,
| 1 |
| 2 |
| 1 |
| 2 |
故只要a≥2-4ln2,函数f(x)在区间(0,
| 1 |
| 2 |
点评:该题考查利用导数研究函数的单调性、最值,考查函数的零点及函数恒成立问题,考查学生对问题的转化能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
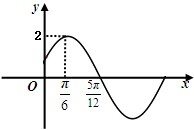 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<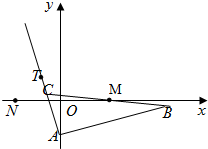 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.