题目内容
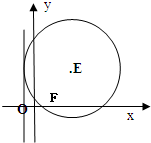 动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C.
动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C.(1)求曲线C的方程;
(2)过点Q(4,2)的任意一条不过点P(4,4)的直线与曲线C交于A,B两点,直线AB与直线y=x+4交于点M,记直线PA,PB,PM的斜率分别为k1,k2,k3,问是否存在实数λ,使得k1+k2=λk3恒成立?若存在,求出λ的值,若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件得曲线C是以A为焦点的抛物线,由此能求出曲线C的方程为y2=4x.
(Ⅱ)设直线AB为y-2=k(x-4).由
,得M(
,
).k3=
.设A(x1,y1),B(x2,y2).由
,得k2x2-(8k2-4k+4)x+16k2-16k+4=0.由此能求出k1+k2=2k3.
(Ⅱ)设直线AB为y-2=k(x-4).由
|
| 4k+2 |
| k-1 |
| 8k-2 |
| k-1 |
| 2k+1 |
| 3 |
|
解答:
 解:(Ⅰ)∵点E到A的距离与到直线x=-1的距离相等,
解:(Ⅰ)∵点E到A的距离与到直线x=-1的距离相等,
∴曲线C是以A为焦点的抛物线.
设为y2=2px,p>0,则
=1,解得p=2,
故曲线C的方程为y2=4x.…(4分)
(Ⅱ)设直线AB的斜率为k,则直线AB的方程为y-2=k(x-4).
由
,得M(
,
).
∴k3=
=
.…(6分)
设A(x1,y1),B(x2,y2).由
,
得k2x2-(8k2-4k+4)x+16k2-16k+4=0.
∴x1+x2=
,x1x2=
.…(8分)
∴k1+k2=
+
=
+
=2k-2(
+
)
=2k-
=2k-
=
.…(11分)
∴k1+k2=2k3,即λ=2.…(13分)
 解:(Ⅰ)∵点E到A的距离与到直线x=-1的距离相等,
解:(Ⅰ)∵点E到A的距离与到直线x=-1的距离相等,∴曲线C是以A为焦点的抛物线.
设为y2=2px,p>0,则
| p |
| 2 |
故曲线C的方程为y2=4x.…(4分)
(Ⅱ)设直线AB的斜率为k,则直线AB的方程为y-2=k(x-4).
由
|
| 4k+2 |
| k-1 |
| 8k-2 |
| k-1 |
∴k3=
4-
| ||
4-
|
| 2k+1 |
| 3 |
设A(x1,y1),B(x2,y2).由
|
得k2x2-(8k2-4k+4)x+16k2-16k+4=0.
∴x1+x2=
| 8k2-4k+4 |
| k2 |
| 16k2-16k+4 |
| k2 |
∴k1+k2=
| y1-4 |
| x1-4 |
| y2-4 |
| x2-4 |
| k(x1-4)-2 |
| x1-4 |
| k(x2-4)-2 |
| x2-4 |
=2k-2(
| 1 |
| x1-4 |
| 1 |
| x2-4 |
=2k-
| 2(x1+x2-8) |
| x1x2-4(x1+x2)+16 |
=2k-
2(
| ||||
|
=
| 4k+2 |
| 3 |
∴k1+k2=2k3,即λ=2.…(13分)
点评:本题考查曲线方程的求法,考查是否存在实数λ,使得k1+k2=λk3恒成立的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
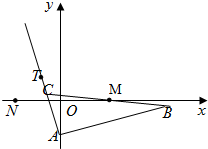 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.