题目内容
下列四个命题中,真命题的是 (写出所有正确的序号).
①若f(x)=2f(2-x)-3x+2(x∈R),则f(x)在点P(1,f(1))处的切线方程为x+y-2=0;
②若对?n∈N*,F(n)>n+1可以推出F(n+1)>n+2,那么F(5)≤6可以推出F(4)≤5;
③若a+b+c>0,ab+bc+ac>0,abc>0,则a>0,b>0,c>0;
④已知A(7,0),B(-7,0),C(2,-12),椭圆过A,B两点且以C为其一个焦点,则椭圆的另一个焦点的轨迹为双曲线;
⑤方程(x2+3y2-9)
=0表示的曲线是一条直线和一个椭圆.
①若f(x)=2f(2-x)-3x+2(x∈R),则f(x)在点P(1,f(1))处的切线方程为x+y-2=0;
②若对?n∈N*,F(n)>n+1可以推出F(n+1)>n+2,那么F(5)≤6可以推出F(4)≤5;
③若a+b+c>0,ab+bc+ac>0,abc>0,则a>0,b>0,c>0;
④已知A(7,0),B(-7,0),C(2,-12),椭圆过A,B两点且以C为其一个焦点,则椭圆的另一个焦点的轨迹为双曲线;
⑤方程(x2+3y2-9)
| x+y-1 |
考点:命题的真假判断与应用
专题:函数的性质及应用,不等式的解法及应用,圆锥曲线的定义、性质与方程
分析:①用2-x替换x得:f(2-x)=2f(x)-3(2-x)+2=2f(x)+3x-4,与已知联立,可求得f(x)=2-x,
从而可求得f(x)在点P(1,f(1))处的切线方程,继而可作出判断;
②利用归纳推理,可判断②正确;
③利用反证法可证得,结论成立;
④利用椭圆的定义,可判断椭圆的另一个焦点的轨迹为双曲线的左支,从而可知④的正误;
⑤由x+y-1≥0,可知该方程表示的是直线y=1-x与其右侧的椭圆(椭圆x2+3y2=9的一部分),从而可判断其正误.
从而可求得f(x)在点P(1,f(1))处的切线方程,继而可作出判断;
②利用归纳推理,可判断②正确;
③利用反证法可证得,结论成立;
④利用椭圆的定义,可判断椭圆的另一个焦点的轨迹为双曲线的左支,从而可知④的正误;
⑤由x+y-1≥0,可知该方程表示的是直线y=1-x与其右侧的椭圆(椭圆x2+3y2=9的一部分),从而可判断其正误.
解答:
解:①∵f(x)=2f(2-x)-3x+2,(1)
∴用2-x替换x得:f(2-x)=2f(x)-3(2-x)+2=2f(x)+3x-4,(2)
联立(1)(2)得:f(x)=2-x,
∴f′(x)=-1,又f(1)=1,
∴f(x)在点P(1,f(1))处的切线方程为:y-1=(x-1),整理得:x+y-2=0,故①正确;
②对?n∈N*,F(n)>n+1可以推出F(n+1)>n+2,那么F(5)≤6可以推出F(4)≤5,正确;
③正确,下面用反证法证明:
显然a,b,c都不为0,
若a<0,
则由abc>0,有bc<0,b,c异号,不妨设b<0,c>0,
∵a+b+c=-|a|-|b|+c>0,∴|a|+|b|<c;
又ab+bc+ac=|a||b|-|b|c-|a|c=|a||b|-(|a|+|b|)c>0,
∴c<
,
∴|a|+|b|<c<
,
即(|a|+|b|)2<|a||b|,
∴a2+b2+|ab|<0,这是不可能的.
∴假设错误,∴a>0,同理b>0,c>0,故③正确;
④设另一个焦点D(x,y),则由椭圆定义知:AC+AD=BC+BD,
∵AC=15,BC=13,
∴BD-AD=AC-BC=2,
∴这是以AB为焦点的双曲线的左支,其方程为:x2-
=1(x<0),故④错误;
⑤方程(x2+3y2-9)
=0中,x+y-1≥0,
故该方程表示的是直线y=1-x与其右侧的椭圆(椭圆x2+3y2=9的一部分),故⑤错误;
综上所述,真命题的是①②③,
故答案为:①②③.
∴用2-x替换x得:f(2-x)=2f(x)-3(2-x)+2=2f(x)+3x-4,(2)
联立(1)(2)得:f(x)=2-x,
∴f′(x)=-1,又f(1)=1,
∴f(x)在点P(1,f(1))处的切线方程为:y-1=(x-1),整理得:x+y-2=0,故①正确;
②对?n∈N*,F(n)>n+1可以推出F(n+1)>n+2,那么F(5)≤6可以推出F(4)≤5,正确;
③正确,下面用反证法证明:
显然a,b,c都不为0,
若a<0,
则由abc>0,有bc<0,b,c异号,不妨设b<0,c>0,
∵a+b+c=-|a|-|b|+c>0,∴|a|+|b|<c;
又ab+bc+ac=|a||b|-|b|c-|a|c=|a||b|-(|a|+|b|)c>0,
∴c<
| |a||b| |
| (|a|+|b|) |
∴|a|+|b|<c<
| |a||b| |
| (|a|+|b|) |
即(|a|+|b|)2<|a||b|,
∴a2+b2+|ab|<0,这是不可能的.
∴假设错误,∴a>0,同理b>0,c>0,故③正确;
④设另一个焦点D(x,y),则由椭圆定义知:AC+AD=BC+BD,
∵AC=15,BC=13,
∴BD-AD=AC-BC=2,
∴这是以AB为焦点的双曲线的左支,其方程为:x2-
| y2 |
| 48 |
⑤方程(x2+3y2-9)
| x+y-1 |
故该方程表示的是直线y=1-x与其右侧的椭圆(椭圆x2+3y2=9的一部分),故⑤错误;
综上所述,真命题的是①②③,
故答案为:①②③.
点评:本题考查求曲线的方程及切线方程,考查归纳推理、反证法、椭圆的概念及应用,考查综合分析与运算求解能力,属于难题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
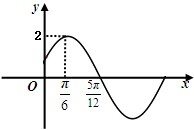 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<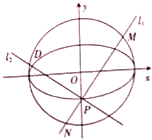 已知椭圆E:
已知椭圆E: