题目内容
已知复数z1=
i和复数z2=
-
i,则复数z1•
的值为( )
| 3 |
| 1 |
| 2 |
| ||
| 6 |
. |
| z2 |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则和共轭复数的定义即可得出.
解答:
解:复数z2=
-
i,∴
=
+
i.
∴复数z1•
=
i•(
+
i)=
i-
.
故选:A.
| 1 |
| 2 |
| ||
| 6 |
| z2 |
| 1 |
| 2 |
| ||
| 6 |
∴复数z1•
. |
| z2 |
| 3 |
| 1 |
| 2 |
| ||
| 6 |
| ||
| 2 |
| 1 |
| 2 |
故选:A.
点评:本题考查了复数的运算法则和共轭复数的定义,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
抛物线y2=2px(p>0)的焦点为F,A为抛物线上一点,则以A为圆心,AF为半径的圆与抛物线的准线的位置关系为( )
| A、相交 | B、相切 |
| C、相离 | D、以上都有可能 |
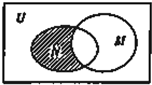 设全集U为实数集R,M={x|x>2},N={x|x<4},则图中阴影部分所表示的集合是( )
设全集U为实数集R,M={x|x>2},N={x|x<4},则图中阴影部分所表示的集合是( )| A、{x|x≤2} |
| B、{x|x≥4} |
| C、{x|x<2} |
| D、{x|2<x<4} |
已知数列{an}中,an-an-1=2(n≥2),且a1=1,则此数列的第10项是( )
| A、18 | B、19 | C、20 | D、21 |
平面向量
与
的夹角为150°,
=(2,0),|
|=2,则|
+
|=( )
| a |
| b |
| a |
| b |
| a |
| 3 |
| b |
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
已知A(1,1),B(3,5),则直线AB的垂直平分线为( )
| A、x-2y-8=0 |
| B、2x+y+8=0 |
| C、x+2y-8=0 |
| D、2x-y-8=0 |
 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )



 2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为
2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为