题目内容
已知椭圆C1:
+
=1的左焦点为F,点P为椭圆上一动点,过点P向以F为圆心,1为半径的圆作切线PM、PN,其中切点为M、N,则四边形PMFN面积的最大值为( )
| x2 |
| 16 |
| y2 |
| 15 |
A、2
| ||
B、
| ||
C、
| ||
| D、5 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由切线的性质可得S四边形PMFN=2×
|FM|•|PM|=|PM|.因此要使四边形PMFN面积取得最大值,|PM|必须取得最大值,因此|PF|必须取得最大值,当P点为椭圆的右顶点时,|PF|取得最大值a+c.
| 1 |
| 2 |
解答:
解:如图所示,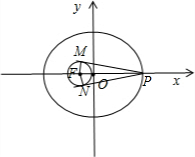
由椭圆C1:
+
=1可得a=4,c=
=1,
∴F(-1,0).
由切线PM、PN,可得PM⊥MF,PN⊥FN.
S四边形PMFN=2×
|FM|•|PM|=|PM|.
因此要使四边形PMFN面积取得最大值,
则|PM|必须取得最大值,因此|PF|必须取得最大值,
当P点为椭圆的右顶点时,|PF|取得最大值a+c=4+1=5.
∴边形PMFN面积最大值为5.
故选:D.

由椭圆C1:
| x2 |
| 16 |
| y2 |
| 15 |
| a2-b2 |
∴F(-1,0).
由切线PM、PN,可得PM⊥MF,PN⊥FN.
S四边形PMFN=2×
| 1 |
| 2 |
因此要使四边形PMFN面积取得最大值,
则|PM|必须取得最大值,因此|PF|必须取得最大值,
当P点为椭圆的右顶点时,|PF|取得最大值a+c=4+1=5.
∴边形PMFN面积最大值为5.
故选:D.
点评:本题考查了椭圆与圆的标准方程及其性质、圆的切线的性质、勾股定理、三角形的面积计算公式,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
设某种动物的体重y(单位:千克)与身长x(单位:厘米)具有线性相关关系,根据一组样本数据建立的回归直线方程为
=0.85x-85.71,则下列结论中不正确的是( )
 |
| y |
| A、y与x具有正的线性相关关系 | ||||
B、回归直线必定经过样本中心点(
| ||||
| C、若某一种该种动物身长增加1厘米,则其体重必定为0.85千克 | ||||
| D、若某一只该种动物身长170厘米,则其体重必定为58.79千克 |
已知复数z1=
i和复数z2=
-
i,则复数z1•
的值为( )
| 3 |
| 1 |
| 2 |
| ||
| 6 |
. |
| z2 |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设变量x,y满足约束条件
,则z=x2-x+y2的最小值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、-
|




