题目内容
 2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为
2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为
| ||
| 2 |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:先在△BCD中,求得BC的长,再求得AC的长,最后在△ABC中利用余弦定理,即可求得AB的长,从而可得结论.
解答:
解:在△BDC中,∠DBC=180°-30°-105°=45°,
所以,由正弦定理得:BC=
=
a.
在△ADC中,∠DAC=180°-60°-60°=60°,
所以,AC=DC=
a.
因此,在△ACB中由余弦定理得:AB=
所以,由正弦定理得:BC=
| DCsin30° |
| sin45° |
| ||
| 4 |
在△ADC中,∠DAC=180°-60°-60°=60°,
所以,AC=DC=
| ||
| 2 |
因此,在△ACB中由余弦定理得:AB=
| AC2+BC2-2AC•BCcos45° |
|
点评:本题重点考查正弦定理与余弦定理的运用,选择三角形,合理运用定理是解题的关键.

练习册系列答案
相关题目
已知复数z1=
i和复数z2=
-
i,则复数z1•
的值为( )
| 3 |
| 1 |
| 2 |
| ||
| 6 |
. |
| z2 |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|

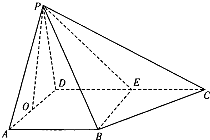 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量