题目内容
如图，梯形ABCD中，AB∥DC，DE⊥AB，CF⊥AB，且AE=EF=FB=5，DE=12，动点P从点A出发，沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止，设运动时间为t秒，y=S△EPF，则y与t的函数图象大致是（ ）A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：分三段考虑，①点P在AD上运动，②点P在DC上运动，③点P在BC上运动，分别求出y与t的函数表达式，继而可得出函数图象．
解答：
解：在Rt△ADE中，AD=
=13，在Rt△CFB中，BC=
=13，
①点P在AD上运动：
过点P作PM⊥AB于点M，则PM=APsin∠A=
t，
此时y=
EF×PM=
t，为一次函数；
②点P在DC上运动，y=
EF×DE=30；
③点P在BC上运动，过点P作PN⊥AB于点N，则PN=BPsin∠B=
（AD+CD+BC-t）=
，
则y=EF×PN=
，为一次函数．
综上可得选项A的图象符合．
故选A．
| AE2+DE2 |
| BF2+CF2 |
①点P在AD上运动：
过点P作PM⊥AB于点M，则PM=APsin∠A=
| 12 |
| 13 |
此时y=
| 1 |
| 2 |
| 30 |
| 13 |
②点P在DC上运动，y=
| 1 |
| 2 |
③点P在BC上运动，过点P作PN⊥AB于点N，则PN=BPsin∠B=
| 12 |
| 13 |
| 12(31-t) |
| 13 |
则y=EF×PN=
| 12(31-t) |
| 13 |
综上可得选项A的图象符合．
故选A．
点评：本题考查了动点问题的函数图象，解答本题的关键是分段讨论y与t的函数关系式，当然在考试过程中，建议同学们直接判断是一次函数还是二次函数，不需要按部就班的解出解析式．
练习册系列答案
相关题目
若直线（2m2+m-3）x+（m2-m）y=4m-1与直线2x-3y-5=0平行，则实数m的值为（ ）
A、-
| ||
| B、1 | ||
C、1或-
| ||
| D、-1 |
若P（2，-1）为圆
（θ为参数且0≤θ＜2π）的弦的中点，则该弦所在的直线方程为（ ）
|
| A、x-y-3=0 |
| B、x+2y=5 |
| C、x+y-1=0 |
| D、2x-y-5=0 |
下列说法中，正确的是（ ）
| A、命题“若am2＜bm2，则a＜b”的逆命题是真命题 | ||||
| B、在△ABC中，若acosA=bcosB，则△ABC为等腰直角三角形 | ||||
| C、命题“?x∈R，x2-x＞0”的否定是：“?x∈R，x2-x≤0” | ||||
D、为得到函数y=sin（2x-
|
已知复数z1=
i和复数z2=
-
i，则复数z1•
的值为（ ）
| 3 |
| 1 |
| 2 |
| ||
| 6 |
. |
| z2 |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
半圆绕着它的直径所在的直线旋转一周所得的几何体是（ ）
| A、球 | B、球面 |
| C、球或球面 | D、以上均不对 |
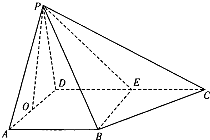如图，在四棱锥P-ABCD中，已知AB⊥AD，PA=PD，D为AD的中点，AB⊥PO，E为线段DC上一点，向量