题目内容
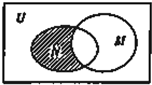设全集U为实数集R，M={x|x＞2}，N={x|x＜4}，则图中阴影部分所表示的集合是（ ）| A、{x|x≤2} |
| B、{x|x≥4} |
| C、{x|x＜2} |
| D、{x|2＜x＜4} |
考点：Venn图表达集合的关系及运算
专题：集合
分析：根据Venn图，得到集合关系为N∩（∁UM），然后根据集合的基本运算求解即可．
解答：
解：由Venn图，得到阴影部分对应的集合为N∩（∁UM），
∵M={x|x＞2}，
∴（∁UM）={x|x≤2}，
∵N={x|x＜4}，
∴N∩（∁UM）={x|x＜4}∩{x|x≤2}={x|x≤2}，
故选：A．
∵M={x|x＞2}，
∴（∁UM）={x|x≤2}，
∵N={x|x＜4}，
∴N∩（∁UM）={x|x＜4}∩{x|x≤2}={x|x≤2}，
故选：A．
点评：本题主要考查集合的基本运算，利用Venn图确定集合关系是解决本题的关键，比较基础．
练习册系列答案
相关题目
有两只水桶，桶1中有a升水，桶2是空桶．现将桶1中的水缓慢注入桶2中，t分钟后桶1中剩余的水符合指数衰减曲线y1=
，桶2中的水就是y2=a-
（k为常数），假设5分钟时，桶1和桶2中的水量相等．从注水开始时，经过m分钟时桶2中的水是桶1中水的3倍，则m=（ ）
| a |
| 2kt |
| a |
| 2kt |
| A、8 | B、10 | C、15 | D、20 |
下列关系中正确的个数为（ ）
①
∈R
②
∉Q
③|-3|∉N*
④|-
|∈Q．
①
| 1 |
| 2 |
②
| 2 |
③|-3|∉N*
④|-
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
设某种动物的体重y（单位：千克）与身长x（单位：厘米）具有线性相关关系，根据一组样本数据建立的回归直线方程为
=0.85x-85.71，则下列结论中不正确的是（ ）
 |
| y |
| A、y与x具有正的线性相关关系 | ||||
B、回归直线必定经过样本中心点（
| ||||
| C、若某一种该种动物身长增加1厘米，则其体重必定为0.85千克 | ||||
| D、若某一只该种动物身长170厘米，则其体重必定为58.79千克 |
在△ABC中，a=
，b=
，A=
，则（ ）
| 5 |
| 15 |
| π |
| 6 |
A、c=2
| ||||
B、c=
| ||||
C、c=2
| ||||
| D、以上都不正确 |
若P（2，-1）为圆
（θ为参数且0≤θ＜2π）的弦的中点，则该弦所在的直线方程为（ ）
|
| A、x-y-3=0 |
| B、x+2y=5 |
| C、x+y-1=0 |
| D、2x-y-5=0 |
设曲线y=x3-3x2+1在点P（1，-1）处的切线与直线ax+y+1=0垂直，则实数a等于（ ）
| A、3 | ||
B、
| ||
| C、-3 | ||
D、-
|
已知复数z1=
i和复数z2=
-
i，则复数z1•
的值为（ ）
| 3 |
| 1 |
| 2 |
| ||
| 6 |
. |
| z2 |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
