题目内容
等差数列{an}前n项和为Sn，a1=1，d=2，则S10=（ ）
| A、70 | B、80 | C、90 | D、100 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：利用等差数列前n项和公式求解．
解答：
解：∵等差数列{an}前n项和为Sn，a1=1，d=2，
∴S10=10+
×2=100．
故选：D．
∴S10=10+
| 10×9 |
| 2 |
故选：D．
点评：本题考查等差数列的前10项和的求法，是基础题，解题时要认真审题，注意等差数列前n项和公式的合理运用．
练习册系列答案
相关题目
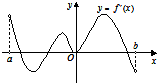函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值（ ）| A、2个 | B、1个 | C、3个 | D、4个 |
设
为复数z的共轭复数，且
•i=1+2i，则z等于（ ）
. |
| z |
. |
| z |
| A、2-i | B、2+i |
| C、1+2i | D、1-2i |
设x，y∈R，向量
=（x，1），
=（1，y），
=（2，-4）且
⊥
，
∥
，则x+y=（ ）
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| A、0 | B、-4 | C、2 | D、4 |
若函数f（x）=|x2-k|的图象与函数g（x）=x-3的图象至多有一个公共点，则实数k的取值范围是（ ）
| A、（-∞，3] |
| B、[9，+∞） |
| C、（0，9] |
| D、（-∞，9] |
tanθ和tan（
-θ）是方程x2+px+q=0的两根，则p与q的关系是（ ）
| π |
| 4 |
| A、p+q+1=0 |
| B、p+q-1=0 |
| C、p-q+1=0 |
| D、p-q-1=0 |
已知Sn为等差数列{an}的前n项和，且满足a2+a2013=32，则log2
=（ ）
| S2014 |
| 2014 |
| A、6 | B、5 | C、4 | D、3 |
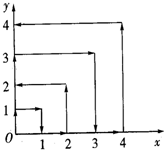如图，一个质点从原点出发，在与y轴．x轴平行的方向按（0，0）→（0，1）→（1，1）→（1，0）→（2，0）→（2，2）…的规律向前移动，且每秒钟移动一个单位长度，那么到第2011秒时，这个质点所处位置的坐标是（ ）| A、（13，44） |
| B、（14，44） |
| C、（44，13） |
| D、（44，14） |
已知sin2α=
，则sin2（α+
）=（ ）
| 2 |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|