题目内容
设
为复数z的共轭复数，且
•i=1+2i，则z等于（ ）
. |
| z |
. |
| z |
| A、2-i | B、2+i |
| C、1+2i | D、1-2i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：把已知的等式变形，然后利用复数代数形式的乘除运算化简，求得
，则复数z可求．
. |
| z |
解答：
解：由
•i=1+2i，得
=
=
=2-i，
∴z=2+i．
故选：B．
. |
| z |
. |
| z |
| 1+2i |
| i |
| (1+2i)(-i) |
| -i2 |
∴z=2+i．
故选：B．
点评：本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
在△ABC中，若tanAtanB=1，则△ABC的形状是（ ）
| A、等边三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
“m=1”是“函数f（x）=x2-6mx+6在区间（-∞，3]上为减函数”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
设奇函数f（x）在（0，+∞）上为单调递增函数，且f（2）=0，则不等式f（x）≥0的解集为（ ）
| A、[-2，0]∪[2，+∞） |
| B、（-∞，-2]∪（0，2] |
| C、（-∞，-2]∪[2，+∞） |
| D、[-2，0）∪（0，2] |
如图，在正方形ABCD中，E为AB中点，BF⊥CE于F，那么S△BFC：S正方形ABCD=（ ）
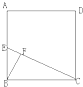
| A、1：3 | B、1：4 |
| C、1：5 | D、1：6 |
函数y=2sinx，x∈[
，
]和y=2的图象围成了一个封闭图形，则此封闭图形的面积是（ ）
| π |
| 2 |
| 5π |
| 2 |
| A、4 | B、2π | C、4π | D、8π |
等差数列{an}前n项和为Sn，a1=1，d=2，则S10=（ ）
| A、70 | B、80 | C、90 | D、100 |
设命题p：函数y=
在定义域上为减函数；命题q：?a，b∈（0，+∞），当a+b=1时，
+
=3，以下说法正确的是（ ）
| 1 |
| x |
| 1 |
| a |
| 1 |
| b |
| A、p∨q为真 | B、p∧q为真 |
| C、p真q假 | D、p，q均假 |