题目内容
设x,y∈R,向量
=(x,1),
=(1,y),
=(2,-4)且
⊥
,
∥
,则x+y=( )
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| A、0 | B、-4 | C、2 | D、4 |
考点:数量积判断两个平面向量的垂直关系,平行向量与共线向量
专题:平面向量及应用
分析:由已知得
,由此能求出x+y=0.
|
解答:
解:∵x,y∈R,向量
=(x,1),
=(1,y),
=(2,-4)且
⊥
,
∥
,
∴
,解得x=2,y=-2,
∴x+y=0.
故选:A.
| a |
| b |
| c |
| a |
| c |
| b |
| c |
∴
|
∴x+y=0.
故选:A.
点评:本题考查代数式的值的求法,是基础题,解题时要注意向量垂直和向量平行的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=sin x+ln x,则f′(1)的值为( )
| A、1-cos 1 |
| B、1+cos 1 |
| C、cos 1-1 |
| D、-1-cos 1 |
“m=1”是“函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
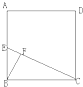
如图,在正方形ABCD中,E为AB中点,BF⊥CE于F,那么S△BFC:S正方形ABCD=( )

| A、1:3 | B、1:4 |
| C、1:5 | D、1:6 |
函数y=2sinx,x∈[
,
]和y=2的图象围成了一个封闭图形,则此封闭图形的面积是( )
| π |
| 2 |
| 5π |
| 2 |
| A、4 | B、2π | C、4π | D、8π |
已知直线l:x+my+4=0,若曲线x2+y2+2x-6y+1=0上存在两点P、Q关于直线l对称,则m的值为( )
| A、2 | B、-2 | C、1 | D、-1 |
等差数列{an}前n项和为Sn,a1=1,d=2,则S10=( )
| A、70 | B、80 | C、90 | D、100 |
与-525°的终边相同的角可表示为( )
| A、525°-k•360°(k∈Z) |
| B、165°+k•360°(k∈Z) |
| C、195°+k•360°(k∈Z) |
| D、-195°+k•360°(k∈Z) |
下列不等式中正确的是( )
A、若a,b∈R,则
| ||||||||||
B、若x,y都是正数,则lgx+lgy≥2
| ||||||||||
C、若x<0,则x+
| ||||||||||
D、若x≤0,则2x+2-x≥2
|