题目内容
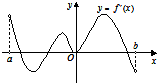函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值（ ）| A、2个 | B、1个 | C、3个 | D、4个 |
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：如图所示，由导函数f′（x）在（a，b）内的图象和极值的定义可知：函数f（x）只有在点B处取得极小值．
解答：
解：如图所示，
由导函数f′（x）在（a，b）内的图象可知：
函数f（x）只有在点B处取得极小值，
∵在点B的左侧f′（x）＜0，右侧f′（x）＞0，且f′（xB）=0．
∴函数f（x）在点B处取得极小值．
故选：B．
由导函数f′（x）在（a，b）内的图象可知：
函数f（x）只有在点B处取得极小值，
∵在点B的左侧f′（x）＜0，右侧f′（x）＞0，且f′（xB）=0．
∴函数f（x）在点B处取得极小值．
故选：B．
点评：本题考查了利用导数研究函数的单调性极值，考查了数形结合的思想方法，考查了推理能力，属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
已知函数f（x）=sin x+ln x，则f′（1）的值为（ ）
| A、1-cos 1 |
| B、1+cos 1 |
| C、cos 1-1 |
| D、-1-cos 1 |
在△ABC中，若tanAtanB=1，则△ABC的形状是（ ）
| A、等边三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
“m=1”是“函数f（x）=x2-6mx+6在区间（-∞，3]上为减函数”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
等差数列{an}前n项和为Sn，a1=1，d=2，则S10=（ ）
| A、70 | B、80 | C、90 | D、100 |