题目内容
tanθ和tan(
-θ)是方程x2+px+q=0的两根,则p与q的关系是( )
| π |
| 4 |
| A、p+q+1=0 |
| B、p+q-1=0 |
| C、p-q+1=0 |
| D、p-q-1=0 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:利用一元二次方程的根与系数的关系、两角和差的正切公式即可得出.
解答:
解:∵tanθ和tan(
-θ)是方程x2+px+q=0的两根,
∴-p=tanθ+tan(
-θ),tanθtan(
-θ)=q.
∴-p=tanθ+
=
,
q=
=
.
∴-p+q=1,
∴p-q+1=0.
故选:C.
| π |
| 4 |
∴-p=tanθ+tan(
| π |
| 4 |
| π |
| 4 |
∴-p=tanθ+
| 1-tanθ |
| 1+tanθ |
| 1+tan2θ |
| 1+tanθ |
q=
| tanθ(1-tanθ) |
| 1+tanθ |
| tanθ-tan2θ |
| 1+tanθ |
∴-p+q=1,
∴p-q+1=0.
故选:C.
点评:本题考查了一元二次方程的根与系数的关系、两角和差的正切公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
如图,在正方形ABCD中,E为AB中点,BF⊥CE于F,那么S△BFC:S正方形ABCD=( )
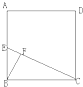

| A、1:3 | B、1:4 |
| C、1:5 | D、1:6 |
已知直线l:x+my+4=0,若曲线x2+y2+2x-6y+1=0上存在两点P、Q关于直线l对称,则m的值为( )
| A、2 | B、-2 | C、1 | D、-1 |
等差数列{an}前n项和为Sn,a1=1,d=2,则S10=( )
| A、70 | B、80 | C、90 | D、100 |
已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次数,求P(ξ=4)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
与-525°的终边相同的角可表示为( )
| A、525°-k•360°(k∈Z) |
| B、165°+k•360°(k∈Z) |
| C、195°+k•360°(k∈Z) |
| D、-195°+k•360°(k∈Z) |
函数y=
的定义域是( )
| ||
| tanx |
A、{x|2kπ≤x≤2kπ+
| ||||
B、{x|2kπ<x<2kπ+
| ||||
| C、{x|2kπ<x<2kπ+π,k∈Z} | ||||
D、{x|2kπ-
|
等差数列{an}的前n项和为Sn,若a1+a3+a8=9,a6=9,则S9的值是( )
| A、64 | B、72 |
| C、54 | D、以上都不对 |