题目内容
若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,则实数k的取值范围是( )
| A、(-∞,3] |
| B、[9,+∞) |
| C、(0,9] |
| D、(-∞,9] |
考点:函数的图象
专题:函数的性质及应用
分析:①当k≤0时,联立方程组,根据判别式△<0,可得两个函数的图象无交点,故满足条件.②当k>0时,在同一个坐标系中,画出这两个函数的图,
如图所示:数形结合可得 0<
≤3,由此求得k的范围.综合①②可得k的范围.
如图所示:数形结合可得 0<
| k |
解答:
 解::①当k≤0时,函数f(x)=|x2-k|=x2-k,由y
解::①当k≤0时,函数f(x)=|x2-k|=x2-k,由y
,可得x2-3x+3-k=0.
由于判别式△=1-4(3-k)=-11+4k<0,故x2-3x+3-k=0无解,
故函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象无交点,故满足条件.
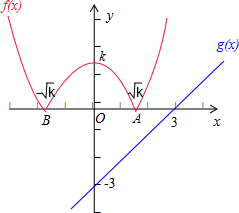
②当k>0时,在同一个坐标系中,画出函数f(x)=|x2-k|的图象(红线部分)
与函数g(x)=x-3的图象(蓝线部分),
如图所示:
此时,若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,
则有 0<
≤3,∴0<k≤9.
综合①②可得,k≤9,
故选 D.
 解::①当k≤0时,函数f(x)=|x2-k|=x2-k,由y
解::①当k≤0时,函数f(x)=|x2-k|=x2-k,由y
|
由于判别式△=1-4(3-k)=-11+4k<0,故x2-3x+3-k=0无解,
故函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象无交点,故满足条件.
②当k>0时,在同一个坐标系中,画出函数f(x)=|x2-k|的图象(红线部分)
与函数g(x)=x-3的图象(蓝线部分),
如图所示:
此时,若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,
则有 0<
| k |
综合①②可得,k≤9,
故选 D.
点评:本题主要考查两个函数的图象的交点个数的判断,体现了分类讨论以及数形结合的数学思想,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
设奇函数f(x)在(0,+∞)上为单调递增函数,且f(2)=0,则不等式f(x)≥0的解集为( )
| A、[-2,0]∪[2,+∞) |
| B、(-∞,-2]∪(0,2] |
| C、(-∞,-2]∪[2,+∞) |
| D、[-2,0)∪(0,2] |
函数y=2sinx,x∈[
,
]和y=2的图象围成了一个封闭图形,则此封闭图形的面积是( )
| π |
| 2 |
| 5π |
| 2 |
| A、4 | B、2π | C、4π | D、8π |
定义在(0,+∞)上的函数f(x)满足:f(2x)=2f(x),且当x∈(1,2]时,f(x)=2-x,若x1,x2是方程f(x)=a(0<a≤1)的两个实数根,则x1-x2不可能是( )
| A、24 | B、72 | C、96 | D、120 |
等差数列{an}前n项和为Sn,a1=1,d=2,则S10=( )
| A、70 | B、80 | C、90 | D、100 |
已知等差数列{an}中,a1+a2+a3+a4+a5=100,则a3=( )
| A、10 | B、20 | C、30 | D、40 |
已知点P(x,y)的坐标满足
,则(x-1)2+y2的取值范围是( )
|
A、[
| ||
B、[
| ||
| C、[1,9) | ||
D、[
|
下列不等式中,正确的是( )
A、tan
| ||||
B、sin
| ||||
| C、sin(π-1)<sin1° | ||||
D、cos
|