题目内容
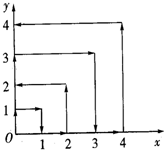 如图,一个质点从原点出发,在与y轴.x轴平行的方向按(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,2)…的规律向前移动,且每秒钟移动一个单位长度,那么到第2011秒时,这个质点所处位置的坐标是( )
如图,一个质点从原点出发,在与y轴.x轴平行的方向按(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,2)…的规律向前移动,且每秒钟移动一个单位长度,那么到第2011秒时,这个质点所处位置的坐标是( )| A、(13,44) |
| B、(14,44) |
| C、(44,13) |
| D、(44,14) |
考点:归纳推理
专题:推理和证明
分析:通过观察和归纳要知道所有偶数的平方均在x轴上,且坐标为k,便对应第k2个点,且从k2向上走k个点就转向左边;所有奇数的平方均在y轴上,且坐标为k,便对应第k2个点,且从k2向右走k个点就转向下边,计算可知2011=442+75,从而可求结果.
解答:
解:由观察及归纳得到,箭头指向x轴的点从左到右依次为:0,3,4,15,16,35,36…
我们所关注的是所有偶数的平方均在x轴上,且坐标为k,便对应第k2个点,且从k2向上走k个点就转向左边,如22向上走2便转向;
箭头指向y轴的点依次为:0,1,8,9,24,25…
我们所关注的是所有奇数的平方均在y轴上,且坐标为k,便对应第k2个点,且从k2向右走k个点就转向下边,如
52向右走5便转向;
因为2011=442+75,所以先找到(44,0)这是第1936个点,还有75步,向上走44步左转,再走31步到达,距y轴有44-31=13个单位,
所以第2009秒时质点所在位置的坐标是(13,44).
故选:A
我们所关注的是所有偶数的平方均在x轴上,且坐标为k,便对应第k2个点,且从k2向上走k个点就转向左边,如22向上走2便转向;
箭头指向y轴的点依次为:0,1,8,9,24,25…
我们所关注的是所有奇数的平方均在y轴上,且坐标为k,便对应第k2个点,且从k2向右走k个点就转向下边,如
52向右走5便转向;
因为2011=442+75,所以先找到(44,0)这是第1936个点,还有75步,向上走44步左转,再走31步到达,距y轴有44-31=13个单位,
所以第2009秒时质点所在位置的坐标是(13,44).
故选:A
点评:本题主要考查了学生观察和归纳能力,会从所给的数据和图形中寻求规律进行解题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
“m=1”是“函数f(x)=x2-6mx+6在区间(-∞,3]上为减函数”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
等差数列{an}前n项和为Sn,a1=1,d=2,则S10=( )
| A、70 | B、80 | C、90 | D、100 |
与-525°的终边相同的角可表示为( )
| A、525°-k•360°(k∈Z) |
| B、165°+k•360°(k∈Z) |
| C、195°+k•360°(k∈Z) |
| D、-195°+k•360°(k∈Z) |
已知点P(x,y)的坐标满足
,则(x-1)2+y2的取值范围是( )
|
A、[
| ||
B、[
| ||
| C、[1,9) | ||
D、[
|
函数y=
的定义域是( )
| ||
| tanx |
A、{x|2kπ≤x≤2kπ+
| ||||
B、{x|2kπ<x<2kπ+
| ||||
| C、{x|2kπ<x<2kπ+π,k∈Z} | ||||
D、{x|2kπ-
|
设命题p:函数y=
在定义域上为减函数;命题q:?a,b∈(0,+∞),当a+b=1时,
+
=3,以下说法正确的是( )
| 1 |
| x |
| 1 |
| a |
| 1 |
| b |
| A、p∨q为真 | B、p∧q为真 |
| C、p真q假 | D、p,q均假 |
下列不等式中正确的是( )
A、若a,b∈R,则
| ||||||||||
B、若x,y都是正数,则lgx+lgy≥2
| ||||||||||
C、若x<0,则x+
| ||||||||||
D、若x≤0,则2x+2-x≥2
|