题目内容
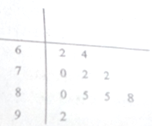 为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.
为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.(1)求这10名群众幸福指数的中位数及平均数;(茎表示十位数字,叶表示个位数字)
(2)若某人的幸福指数在[70,80)内,称该人为“一般幸福”人;在[80,90)内,称该人为“较幸福”的人,现分别从这10名群众的“一般幸福”人和“较幸福”人中各抽取1人,求他们的幸福指数的和超过155的概率.
考点:古典概型及其概率计算公式,众数、中位数、平均数,极差、方差与标准差
专题:概率与统计
分析:(1)由茎叶图知中位数为76,将各个数代入平均数公式求出平均数;
(2)列举出该随机试验的基本事件总数及幸福指数超过155的基本事件个数,代入古典概型的概率公式求出概率.
(2)列举出该随机试验的基本事件总数及幸福指数超过155的基本事件个数,代入古典概型的概率公式求出概率.
解答:
解:(1)由茎叶图知中位数为76,
平均数=
=77
(2)该随机试验的基本事件有:(70,80),(70,85),(70,85),(70,88),(72,80)(72,85),(72,85),(72,88)(72,80)(72,85),(72,85),(72,88)共12个,
其中幸福指数超过155的基本事件有:(70,88),(72,85),(72,85),(72,88),(72,85),(72,85),(72,88)共7个,
记“他们的幸福指数的和超过155”为事件A,
则P(A)=
平均数=
| 62+64+70+72+72+80+85+85+88+92 |
| 10 |
(2)该随机试验的基本事件有:(70,80),(70,85),(70,85),(70,88),(72,80)(72,85),(72,85),(72,88)(72,80)(72,85),(72,85),(72,88)共12个,
其中幸福指数超过155的基本事件有:(70,88),(72,85),(72,85),(72,88),(72,85),(72,85),(72,88)共7个,
记“他们的幸福指数的和超过155”为事件A,
则P(A)=
| 7 |
| 12 |
点评:本题考查由茎叶图求数据的中位数,平均数;考查古典概型的概率公式,属于一道基础题.

练习册系列答案
相关题目
已知集合U={0,1,2,3,4},A={x|x2-2x=0},则∁UA=( )
| A、{1,2,3} |
| B、{0,1,3,4} |
| C、{1,3,4} |
| D、{0,3,4} |
圆(x-1)2+(y-1)2=1关于直线y=5x-4对称的圆的方程是( )
| A、(x+1)2+(y+1)2=1 |
| B、(x-1)2+(y-1)2=1 |
| C、(x+1)2+(y-1)2=1 |
| D、(x-1)2+(y+1)2=1 |
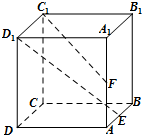 已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点,点M、N分别是线段D1E与C1F上的点,则满足与平面ABCD平行的直线MN有( )
已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点,点M、N分别是线段D1E与C1F上的点,则满足与平面ABCD平行的直线MN有( )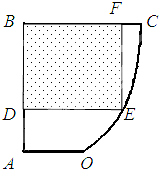 某同学的数学研究性学习课题是:在校内一块不规则土地OABC(测绘图如图所示)规划一个矩形运动场地.经过测量发现AB⊥BC,OA∥BC,曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段,OA=20m,AB=BC=40m.
某同学的数学研究性学习课题是:在校内一块不规则土地OABC(测绘图如图所示)规划一个矩形运动场地.经过测量发现AB⊥BC,OA∥BC,曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段,OA=20m,AB=BC=40m.