题目内容
将一个骰子先后抛掷两次，事件A表示“第一次出现奇数点”，事件B表示“第二次的点数不小于5”，则P（A+B）= ．
考点：互斥事件的概率加法公式
专题：概率与统计
分析：根据概率即计算公式，先求出事件A，B都没有发生的，再根据互斥事件的概率公式计算即可．
解答：
解：事件A+B也就是A∪B，它表示A发生或B发生，即A，B至少有一个发生，将一个骰子先后抛掷两次，
基本事件总数是36个，其中第一次不出现奇数点且第二次的点数小于5有12种
∴事件A，B都没有发生的概率为
=
，
∴P（A+B）=1-
=
．
故答案为：
．
基本事件总数是36个，其中第一次不出现奇数点且第二次的点数小于5有12种
∴事件A，B都没有发生的概率为
| 12 |
| 36 |
| 1 |
| 3 |
∴P（A+B）=1-
| 1 |
| 3 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题主要考查了互斥事件的概率加法公式，属于基础题．
练习册系列答案
相关题目
执行如图所示的程序框图，若输入x∈[0，2π]，则输出y的取值范围是（ ）
| A、[0，1] | ||||
| B、[-1，1] | ||||
C、[-
| ||||
D、[-1，
|
已知cosα=
，α是第四象限角，则sinα=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知函数f（x）=sin2x-
cos2x的图象向左平移m（m＞0）个单位后关于y轴对称，则m的最小值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
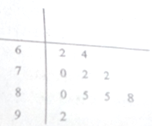为了保护生态和环境，某市不再完全以GDP考核辖区内各县政府的政绩，广大群众的幸福指数成为考核县政府政绩的又一个重要指标，从而成立了市政府幸福办公室，其主要工作是随机抽查群众的幸福指数，为市政府提供最基础的原始数据．该办公室某工作人员在一次随机抽查了10名A县群众后，绘制了如图的茎叶图．