题目内容
若实数x,y满足
,且z=ax+y的最小值为2,则实数a的值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用线性规划的知识,确定目标取最优解的条件,即可求出a的取值范围.
解答:
 解:作出不等式对应的平面区域,
解:作出不等式对应的平面区域,
由z=ax+y得y=-ax+z,
若a=0,则y=z,此时z=ax+y的最小值为0,不满足条件.
若a>0,则y=-ax+z的斜率-a<0.此时直线经过点B(1,0)时取得最小值2,
此时a+0=2,解得a=2,满足条件.
若a<0,则y=-ax+z的斜率-a>0.要是目标函数取得最小值2,
则满足
,即
,此时不满足条件.
综上:a=2,
故答案为:2.
 解:作出不等式对应的平面区域,
解:作出不等式对应的平面区域,由z=ax+y得y=-ax+z,
若a=0,则y=z,此时z=ax+y的最小值为0,不满足条件.
若a>0,则y=-ax+z的斜率-a<0.此时直线经过点B(1,0)时取得最小值2,
此时a+0=2,解得a=2,满足条件.
若a<0,则y=-ax+z的斜率-a>0.要是目标函数取得最小值2,
则满足
|
|
综上:a=2,
故答案为:2.
点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.根据条件目标函数z=ax+y的最小值为2,确定直线的位置是解决本题的关键.

练习册系列答案
相关题目
函数f(x)=
-
( )
| x |
| 1-2x |
| x |
| 2 |
| A、是偶函数,在(-∞,0)上是增函数 |
| B、是偶函数,在(-∞,0)上是减函数 |
| C、是奇函数,在(-∞,0)上是增函数 |
| D、是奇函数,在(-∞,0)上是减函数 |
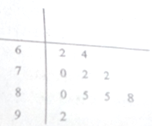 为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.
为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.