题目内容
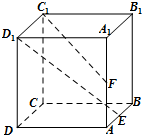已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点，点M、N分别是线段D1E与C1F上的点，则满足与平面ABCD平行的直线MN有（ ）| A、0条 | B、1条 | C、2条 | D、无数条 |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：取BB1的中点H，连接FH，在D1E上任取一点M，过M在面D1HE中，作MG平行于HO，其中O为线段D1E的中点，交D1H于G，再过G作GN∥FH，交C1F于N，连接MN，根据线面平行的判定定理，得到GM∥平面ABCD，NG∥平面ABCD，再根据面面平行的判断定理得到平面MNG∥平面ABCD，由面面平行的性质得到则MN∥平面ABCD，由于M是任意的，故MN有无数条．
解答：
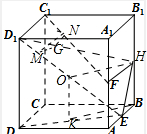解：取BB1的中点H，连接FH，则FH∥C1D，
连接HE，在D1E上任取一点M，
过M在面D1HE中，作MG平行于HO，
其中O为线段D1E的中点，交D1H于G，
再过G作GN∥FH，交C1F于N，连接MN，
O在平面ABCD的正投影为K，连接KB，则OH∥KB，
由于GM∥HO，HO∥KB，KB?平面ABCD，
GM?平面ABCD，
所以GM∥平面ABCD，
同理由NG∥FH，可推得NG∥平面ABCD，
由面面平行的判定定理得，平面MNG∥平面ABCD，
则MN∥平面ABCD．
由于M为D1E上任一点，故这样的直线MN有无数条．
故选：D．
解：取BB1的中点H，连接FH，则FH∥C1D，连接HE，在D1E上任取一点M，
过M在面D1HE中，作MG平行于HO，
其中O为线段D1E的中点，交D1H于G，
再过G作GN∥FH，交C1F于N，连接MN，
O在平面ABCD的正投影为K，连接KB，则OH∥KB，
由于GM∥HO，HO∥KB，KB?平面ABCD，
GM?平面ABCD，
所以GM∥平面ABCD，
同理由NG∥FH，可推得NG∥平面ABCD，
由面面平行的判定定理得，平面MNG∥平面ABCD，
则MN∥平面ABCD．
由于M为D1E上任一点，故这样的直线MN有无数条．
故选：D．
点评：本题考查空间直线与平面的位置关系，主要是直线与平面平行的判断和面面平行的判定与性质，考查空间想象能力和简单推理能力．
练习册系列答案
阅读快车系列答案
相关题目
△ABC中，已知a=
，b=1，C=30°，则△ABC的面积为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各点中不在不等式组
表示的平面区域内的是（ ）
|
| A、（1，1） | ||||
| B、（0，0） | ||||
C、（
| ||||
D、（
|
复数
等于（ ）
| 2i |
| 1+i3 |
| A、1-i | B、-1+i |
| C、1+i | D、-1-i |
已知cosα=
，α是第四象限角，则sinα=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
抛物线y2=16x的焦点坐标是（ ）
| A、（4，0） |
| B、（0，4） |
| C、（8，0） |
| D、（0，8） |
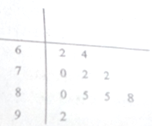为了保护生态和环境，某市不再完全以GDP考核辖区内各县政府的政绩，广大群众的幸福指数成为考核县政府政绩的又一个重要指标，从而成立了市政府幸福办公室，其主要工作是随机抽查群众的幸福指数，为市政府提供最基础的原始数据．该办公室某工作人员在一次随机抽查了10名A县群众后，绘制了如图的茎叶图．
执行如图所示的程序框图，分别输入a2、a+2，相应地输出y1，y2，若y1＞y2，则实数a的取值范围为