题目内容
5.设函数$f(x)=b{x^3}-\frac{3}{2}(2b+1){x^2}+6x+a(b>0)$.(1)求f(x)的单调区间;
(2)设b=1,若方程f(x)=0有且只有一个实根,求a的取值范围.
分析 (1)先求导,再分类讨论即可得到函数的单调区间,
(2)代值,并求导,根据(1)得到函数的单调区间,求出函数的极值,依题意只需f(2)>0或f(1)<0即可.
解答 解:(1)f'(x)=3bx2-3(2b+1)x+6=3(x-2)(bx-1),
令f'(x)=0得x=2或$x=\frac{1}{b}$,
①当$\frac{1}{b}<2$即$b>\frac{1}{2}$时,f(x)在$({-∞,\;\;\frac{1}{b}})$和(2,+∞)上递增,在$({\frac{1}{b},\;\;2})$上递减.
②当$\frac{1}{b}>2$即$0<b<\frac{1}{2}$时,f(x)在(-∞,2)和$({\frac{1}{b},\;\;+∞})$上递增,在$({2,\;\;\frac{1}{b}})$上递减.
③当$\frac{1}{b}=2$即$b=\frac{1}{2}$时,f(x)在R上递增.
(2)b=1时,$f(x)={x^3}-\frac{9}{2}{x^2}+6x+a$,
∴f'(x)=3x2-9x+6=3(x-2)(x-1),
∴f(x)在(-∞,1)和(2,+∞)上递增,在(1,2)上递减,
∴在x=2处取得极小值,在x=1处取得极大值,
∴依题意只需f(2)>0或f(1)<0即可,f(2)=2+a>0,或$f(1)=\frac{5}{2}+a<0$,
∴a>-2或$a<-\frac{5}{2}$.
点评 本题主要考查二次函数的性质、方程的根问题的处理策略,考查利用导数研究函数的极值的知识,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若集合A={-1,1},B={0,1},则集合A∪B的子集个数为( )
| A. | 4 | B. | 5 | C. | 7 | D. | 8 |
13.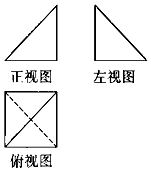 如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
 如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )| A. | $2+4\sqrt{2}+2\sqrt{3}$ | B. | $2+4\sqrt{2}+\sqrt{6}$ | C. | $2+4\sqrt{2}$ | D. | $\frac{4}{3}$ |
10.函数$f(x)=sin(\frac{π}{2}-x)$是( )
| A. | 奇函数,且在区间$(0,\frac{π}{2})$上单调递增 | B. | 奇函数,且在区间$(0,\frac{π}{2})$上单调递减 | ||
| C. | 偶函数,且在区间$(0,\frac{π}{2})$上单调递增 | D. | 偶函数,且在区间$(0,\frac{π}{2})$上单调递减 |
14.已知函数f(x)=ln|ax|(a≠0),g(x)=x-3+sinx,则( )
| A. | f(x)+g(x)是偶函数 | B. | f(x)•g(x)是偶函数 | C. | f(x)+g(x)是奇函数 | D. | f(x)•g(x)是奇函数 |