题目内容
20.定义在[1,e2]上的函数$f(x)=\frac{lnx}{x}$,则对任意的x∈[1,e2],使f(x)单调递减的概率为$\frac{e}{e+1}$.分析 求导数,由f'(x)<0,解得函数在区间(e,e2]上单调递减,即可求出函数f(x)单调递减的概率.
解答 解:$f'(x)=\frac{1-lnx}{x^2}({e^2}≥x≥1)$,由f'(x)≥0,解得函数在区间[1,e]上单调递增,
由f'(x)<0,解得函数在区间(e,e2]上单调递减,所以函数f(x)单调递减的概率$P=\frac{{{e^2}-e}}{{{e^2}-1}}=\frac{e}{e+1}$.
故答案为$\frac{e}{e+1}$.
点评 本题考查几何概型,考查导数知识的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.设集合A={x|x≤-4或x≥2},B={x||x-1|≤3},则等于∁R(A∩B)( )
| A. | [2,4] | B. | [-2,2) | C. | (-∞,2)∪(4,+∞) | D. | (-∞,-4)∪(-2,+∞) |
15.已知tanα=2,则$\frac{{2{{sin}^2}α+1}}{{cos2(α-\frac{π}{4})}}$的值是( )
| A. | $\frac{5}{3}$ | B. | $-\frac{13}{4}$ | C. | $\frac{13}{5}$ | D. | $\frac{13}{4}$ |
5.设函数$f(x)=b{x^3}-\frac{3}{2}(2b+1){x^2}+6x+a(b>0)$.
(1)求f(x)的单调区间;
(2)设b=1,若方程f(x)=0有且只有一个实根,求a的取值范围.
(1)求f(x)的单调区间;
(2)设b=1,若方程f(x)=0有且只有一个实根,求a的取值范围.
12.如图,在△ABC中,点D在线段BC上,且BD=2DC,若$\overrightarrow{AD}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$,则$\frac{λ}{μ}$=( )
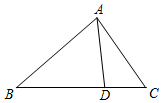

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{2}{3}$ |
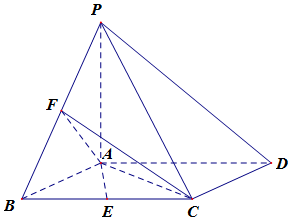 如图所示,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PB的中点.
如图所示,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PB的中点. 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点