题目内容
13．
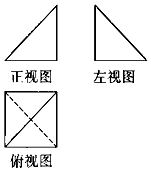如图1，一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2，俯视图是边长为2的正方形，则该多面体的表面积是（ ）| A． | $2+4\sqrt{2}+2\sqrt{3}$ | B． | $2+4\sqrt{2}+\sqrt{6}$ | C． | $2+4\sqrt{2}$ | D． | $\frac{4}{3}$ |
分析 画出几何体的直观图，分析出各个面的形状，求出各个面的面积后，相加可得答案．
解答 
解：该多面体为一个三棱锥D-ABC，
如图1所示，
其中3个面是直角三角形，1个面是等边三角形，
S表面积=S△ABC+S△ABD+S△ACD+S△BCD=$\frac{1}{2}×2×2+\frac{1}{2}×2×2\sqrt{2}+\frac{1}{2}×2×2\sqrt{2}+\frac{1}{2}×2\sqrt{2}×2\sqrt{2}sin60°$=$2+4\sqrt{2}+2\sqrt{3}$，
故选A．
点评 本题考查的知识点是棱锥的表面积和体积，简单几何体的三视图，难度中档．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
3．已知直线m，n和平面α，下列推理正确的是（ ）
| A． | $\left.{\begin{array}{l}{m⊥n}\\{n?α}\end{array}}\right\}⇒m⊥α$ | B． | $\left.{\begin{array}{l}{m⊥n}\\{n⊥α}\end{array}}\right\}⇒m∥α$ | C． | $\left.{\begin{array}{l}{m⊥α}\\{n∥α}\end{array}}\right\}⇒m⊥n$ | D． | $\left.{\begin{array}{l}{m∥α}\\{n?α}\end{array}}\right\}⇒m∥n$ |
4．设函数$f（x）=\sqrt{x-1}$，则$f（\frac{x}{2}）+f（\frac{4}{x}）$的定义域为（ ）
| A． | $[\frac{1}{2}，4]$ | B． | [2，4] | C． | [1，+∞） | D． | [$\frac{1}{4}$，2] |
8．设集合A={x|x≤-4或x≥2}，B={x||x-1|≤3}，则等于∁R（A∩B）（ ）
| A． | [2，4] | B． | [-2，2） | C． | （-∞，2）∪（4，+∞） | D． | （-∞，-4）∪（-2，+∞） |
18．已知函数$f（x）=\left\{\begin{array}{l}lnx，x＞1\\{2^{-x+1}}，x≤1\end{array}\right.$，若方程$f（x）-ax=\frac{5}{2}$有3个不同的解，则a的取值范围是（ ）
| A． | $（-∞，-\frac{5}{2}]$ | B． | $（-\frac{5}{2}，-\frac{3}{2}]$ | C． | $[-\frac{5}{2}，-\frac{3}{2}]$ | D． | $（-\frac{3}{2}，+∞）$ |