题目内容
10.函数$f(x)=sin(\frac{π}{2}-x)$是( )| A. | 奇函数,且在区间$(0,\frac{π}{2})$上单调递增 | B. | 奇函数,且在区间$(0,\frac{π}{2})$上单调递减 | ||
| C. | 偶函数,且在区间$(0,\frac{π}{2})$上单调递增 | D. | 偶函数,且在区间$(0,\frac{π}{2})$上单调递减 |
分析 函数$f(x)=sin(\frac{π}{2}-x)$=cosx,即可得出结论.
解答 解:函数$f(x)=sin(\frac{π}{2}-x)$=cosx,是偶函数,且在区间$(0,\frac{π}{2})$上单调递减,
故选D.
点评 本题考查诱导公式,考查余弦函数的性质,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.为了得到函数y=sin3x-$\sqrt{3}$cos3x的图象( )
| A. | 只要将函数y=2sin3x的图象向右平移$\frac{π}{3}$个单位 | |
| B. | 只要将函数y=sin3x的图象向右平移$\frac{π}{3}$个单位 | |
| C. | 只要将函数y=2sin3x的图象向右平移$\frac{π}{9}$个单位 | |
| D. | 只要将函数y=sin3x的图象向右平移$\frac{π}{9}$个单位 |
18.已知函数$f(x)=\left\{\begin{array}{l}lnx,x>1\\{2^{-x+1}},x≤1\end{array}\right.$,若方程$f(x)-ax=\frac{5}{2}$有3个不同的解,则a的取值范围是( )
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
5.设函数$f(x)=b{x^3}-\frac{3}{2}(2b+1){x^2}+6x+a(b>0)$.
(1)求f(x)的单调区间;
(2)设b=1,若方程f(x)=0有且只有一个实根,求a的取值范围.
(1)求f(x)的单调区间;
(2)设b=1,若方程f(x)=0有且只有一个实根,求a的取值范围.
15.函数$y=2\sqrt{2}sin(ωx+φ)$(其中ω>0,0<φ<π)的图象的一部分如图所示,则( )
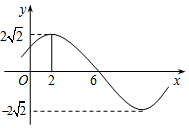

| A. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{3π}{4}$ | B. | $ω=\frac{π}{8}{,_{\;}}φ=\frac{π}{4}$ | C. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{π}{2}$ | D. | $ω=\frac{π}{4}{,_{\;}}φ=\frac{3π}{4}$ |