题目内容
1.等差数列{an}中,a2+a3=9,a4+a5=21,那么它的公差是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据a2+a3=9,a4+a5=21我们构造关于基本量(首项及公差)的方程,解方程求出基本量(首项及公差),即可求解.
解答 解:∵(a4+a5)-(a2+a3)=4d=12,
∴d=3
故选:A.
点评 本题考查了等差数列的性质,此题巧用了(a4+a5)-(a2+a3)直接求出了结果.属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
11.已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{n}{m}$=( )

| A. | 1 | B. | 3 | C. | $\frac{8}{3}$ | D. | $\frac{9}{2}$ |
12.衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,得到下面的数据表:
下面临界值表:
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}},n=a+b+c+d$
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 100 | 120 |
| 女 | 20 | 20 | 40 |
| 合计 | 40 | 120 | 160 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
9.给出下列结论:①$\root{4}{(-2)^{4}}$=±2;②y=x2+1,x∈[-1,2],y的值域是[2,5];③幂函数图象一定不过第四象限;④函数f(x)=ax+1-2(a>0,a≠1)的图象过定点(-1,-1);⑤若lna<1成立,则a的取值范围是(-∞,e).其中正确的序号是( )
| A. | ①② | B. | ③④ | C. | ①④ | D. | ③④⑤ |
13.设集合$A=\left\{{x\left|{\frac{2x+1}{x-2}≤0}\right.}\right\}$,B={x|x<1},则A∪B=( )
| A. | $[{-\frac{1}{2},1})$ | B. | (-1,1)∪(1,2) | C. | (-∞,2) | D. | $[{-\frac{1}{2},2})$ |
11.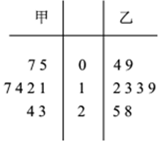 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )| A. | m甲=m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | m甲=m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | m甲>m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | D. | m甲<m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ |
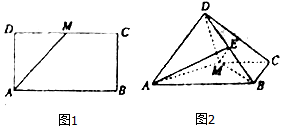 如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.