题目内容
10.已知数列{an}的首项a1=2,数列{bn}为等比数列,且bn=$\frac{{a}_{n+1}}{{a}_{n}}$,又b10b11=2017${\;}^{\frac{1}{10}}$,则a21=4034.分析 由已知结合bn=$\frac{{a}_{n+1}}{{a}_{n}}$,得到a21=b1b2…b20,结合b10b11=2017${\;}^{\frac{1}{10}}$,及等比数列的性质求得a21.
解答 解:由bn=$\frac{{a}_{n+1}}{{a}_{n}}$,且a1=2,得b1=$\frac{{a}_{2}}{{a}_{1}}=\frac{{a}_{2}}{2}$.
b2=$\frac{{a}_{3}}{{a}_{2}}$,a3=a2b2=2b1b2.
b3=$\frac{{a}_{4}}{{a}_{3}}$,a4=a3b3=2b1b2b3.
…
an=2b1b2…bn-1.
∴a21=2b1b2…b20.
∵数列{bn}为等比数列,
∴a21=2(b1b20)(b2b19)…(b10b11)=2$(201{7}^{\frac{1}{10}})^{10}$=4034.
故答案为:4034.
点评 本题考查了数列递推式,考查了等比数列的性质,是中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
1.等差数列{an}中,a2+a3=9,a4+a5=21,那么它的公差是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.执行如图程序,输出S的值为( )
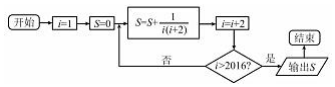

| A. | $\frac{1007}{2015}$ | B. | $\frac{1008}{2017}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2015}{4032}$ |
15.某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.
| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
20.已知变量x与y的取值如表所示,且2.5<n<m<6.5,则由该数据算得的线性回归方程可能是( )
| x | 2 | 3 | 4 | 5 |
| y | 6.5 | m | n | 2.5 |
| A. | $\stackrel{∧}{y}$=0.8x+2.3 | B. | $\stackrel{∧}{y}$=2x+0.4 | C. | $\stackrel{∧}{y}$=-1.5x+8 | D. | $\stackrel{∧}{y}$=-1.6x+10 |
 甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是$\frac{1}{3}$,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是$\frac{1}{3}$,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.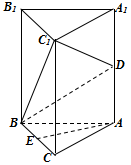 如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.
如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.