题目内容
9.给出下列结论:①$\root{4}{(-2)^{4}}$=±2;②y=x2+1,x∈[-1,2],y的值域是[2,5];③幂函数图象一定不过第四象限;④函数f(x)=ax+1-2(a>0,a≠1)的图象过定点(-1,-1);⑤若lna<1成立,则a的取值范围是(-∞,e).其中正确的序号是( )| A. | ①② | B. | ③④ | C. | ①④ | D. | ③④⑤ |
分析 由根式的化简判断①,根据二次函数的性质判断②,由幂函数的性质判断③,由a0=1和指数函数的判断④,由对数函数的性质判断⑤.
解答 解::①$\root{4}{(-2)^{4}}$=|-2|=2,①不正确;
②y=x2+1,x∈[-1,2],y的值域是[1,5],②不正确;
③由幂函数知:幂函数图象一定不过第四象限,③正确;
④令x+1=0得x=-1,且y=-1,即f(x)=ax+1-2的图象过定点(-1,-1),④正确;
⑤由lna<1得0<a<e,即a的取值范围是(0,e),⑤不正确,
正确的命题是③④,
故选:B.
点评 本题考查基本初等函数的图象与性质,以及根式的化简的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知函数f(x)=$\left\{\begin{array}{l}(3a-2)x+6a-1(x<1)\\{a^x}(x≥1)\end{array}\right.$单调递减,那么实数a的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{2}{3}$) | C. | [$\frac{3}{8}$,$\frac{2}{3}$) | D. | [$\frac{3}{8}$,1) |
4.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(1),则x的取值范围是( )
| A. | $({\frac{1}{10},1})$ | B. | $({\frac{1}{10},10})$ | C. | $({0,\frac{1}{10}})∪({1,+∞})$ | D. | (0,1)∪(10,+∞) |
1.等差数列{an}中,a2+a3=9,a4+a5=21,那么它的公差是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是$\frac{1}{3}$,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是$\frac{1}{3}$,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖. 如图,已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).
如图,已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).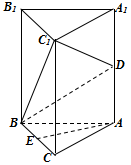 如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.
如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.