题目内容
16.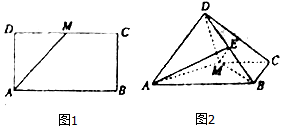 如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.(1)求证:AD⊥BM;
(2)若点E是线段DB上的中点,四棱锥D-ABCM的体积为V,求三棱锥E-ADM的体积.
分析 (1)由题意可得BM⊥AM,再由平面ADM⊥平面ABCM,结合面面垂直的性质可得BM⊥平面ADM,从而得到AD⊥BM;
(2)直接利用等体积法求得三棱锥E-ADM的体积.
解答 (1)证明:∵长方形ABCD中,AB=2AD,M为DC的中点,
∴AM=BM,则BM⊥AM,
∵平面ADM⊥平面ABCM,
平面ADM∩平面ABCM=AM,BM?平面ABCM,
∴BM⊥平面ADM,∵AD?平面ADM,
∴AD⊥BM;
(2)解:当E为DB的中点时,
∵${S}_{△MBC}=\frac{1}{2}{S}_{△MAB}$,
∴${V}_{E-ADM}=\frac{1}{2}{V}_{B-ADM}$=$\frac{1}{2}{V}_{D-ABM}$=$\frac{1}{2}×\frac{2}{3}{V}_{D-ABCM}=\frac{1}{3}{V}_{D-ABCM}$=$\frac{1}{3}V$.
点评 本题考查空间中直线与直线的位置关系,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x}-1,x>0}\\{\frac{3}{2}x+1,x≤0}\end{array}\right.$若m<n,且f(m)=f(n),则n-m的取值范围是( )
| A. | [ln2,ln$\frac{3}{2}$+$\frac{1}{3}$] | B. | (ln2,ln$\frac{3}{2}$+$\frac{1}{3}$) | C. | ($\frac{2}{3}$,ln2] | D. | ($\frac{2}{3}$,ln$\frac{3}{2}$+$\frac{1}{3}$] |
4.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(1),则x的取值范围是( )
| A. | $({\frac{1}{10},1})$ | B. | $({\frac{1}{10},10})$ | C. | $({0,\frac{1}{10}})∪({1,+∞})$ | D. | (0,1)∪(10,+∞) |
1.等差数列{an}中,a2+a3=9,a4+a5=21,那么它的公差是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.执行如图程序,输出S的值为( )
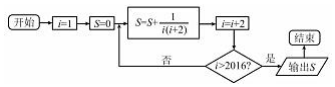

| A. | $\frac{1007}{2015}$ | B. | $\frac{1008}{2017}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2015}{4032}$ |
6.(x2+3x-y)5的展开式中,x5y2的系数为( )
| A. | -90 | B. | -30 | C. | 30 | D. | 90 |