题目内容
13.设集合$A=\left\{{x\left|{\frac{2x+1}{x-2}≤0}\right.}\right\}$,B={x|x<1},则A∪B=( )| A. | $[{-\frac{1}{2},1})$ | B. | (-1,1)∪(1,2) | C. | (-∞,2) | D. | $[{-\frac{1}{2},2})$ |
分析 求出集合A,取A、B的并集即可.
解答 解:$A=\left\{{x\left|{\frac{2x+1}{x-2}≤0}\right.}\right\}$={x|-$\frac{1}{2}$≤x<2},B={x|x<1},
则A∪B=(-∞,2),
故选:C.
点评 本题考查了集合的并集的运算,考查不等式问题,是一道基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
4.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(1),则x的取值范围是( )
| A. | $({\frac{1}{10},1})$ | B. | $({\frac{1}{10},10})$ | C. | $({0,\frac{1}{10}})∪({1,+∞})$ | D. | (0,1)∪(10,+∞) |
1.等差数列{an}中,a2+a3=9,a4+a5=21,那么它的公差是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.执行如图程序,输出S的值为( )
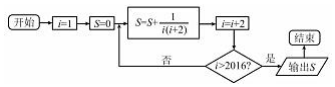

| A. | $\frac{1007}{2015}$ | B. | $\frac{1008}{2017}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2015}{4032}$ |
3.已知函数f(x)=$\sqrt{2}$sinωx+$\sqrt{2}$cosωx(ω>0),在区间(-$\frac{π}{3}$,$\frac{π}{4}$)上单调递增,则ω的取值范围为( )
| A. | (0,1] | B. | [1,2) | C. | [$\frac{1}{3}$,2) | D. | (2,+∞) |