题目内容
11.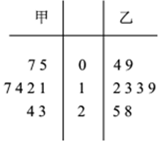 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )| A. | m甲=m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | m甲=m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | m甲>m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | D. | m甲<m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ |
分析 由茎叶图中的数据,计算甲、乙运动员的中位数和平均数,比较得出结论.
解答 解:由已知中茎叶图可得,
甲运动员的成绩分别为:5,7,11,12,14,17,23,24;
故甲的中位数为m甲=$\frac{1}{2}$×(12+14)=13,
平均数为$\overline{{x}_{甲}}$=$\frac{1}{8}$×(5+7+11+12+14+17+23+24)=$\frac{113}{8}$;
乙运动员的成绩分别为:4,9,12,13,13,16,25,28;
故乙的中位数是m乙=$\frac{1}{2}$×(13+13)=13,
平均数是$\overline{{x}_{乙}}$=$\frac{1}{8}$×(4+9+12+13+13+16+25+28)=$\frac{120}{8}$;
∴m甲=m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$.
故选:B.
点评 本题考查了利用茎叶图中的数据计算中位数与平均值的应用问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.等差数列{an}中,a2+a3=9,a4+a5=21,那么它的公差是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.(x2+3x-y)5的展开式中,x5y2的系数为( )
| A. | -90 | B. | -30 | C. | 30 | D. | 90 |
3.已知函数f(x)=$\sqrt{2}$sinωx+$\sqrt{2}$cosωx(ω>0),在区间(-$\frac{π}{3}$,$\frac{π}{4}$)上单调递增,则ω的取值范围为( )
| A. | (0,1] | B. | [1,2) | C. | [$\frac{1}{3}$,2) | D. | (2,+∞) |
20.已知变量x与y的取值如表所示,且2.5<n<m<6.5,则由该数据算得的线性回归方程可能是( )
| x | 2 | 3 | 4 | 5 |
| y | 6.5 | m | n | 2.5 |
| A. | $\stackrel{∧}{y}$=0.8x+2.3 | B. | $\stackrel{∧}{y}$=2x+0.4 | C. | $\stackrel{∧}{y}$=-1.5x+8 | D. | $\stackrel{∧}{y}$=-1.6x+10 |
 如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.
如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.