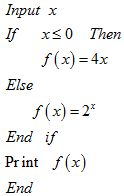题目内容
7.已知函数f(x)=ex-kx+k(k∈R).(1)试讨论函数y=f(x)的单调性;
(2)若该函数有两个不同的零点x1,x2试求实数k取值范围.
分析 (1)求出函数的导数,通过讨论k的范围求出函数的单调区间即可;
(2)结合题意得到k>0时,函数的单调性,从而求出k的范围即可.
解答 解:(1)由f(x)=ex-kx+k,(k∈R),则f′(x)=ex-k,
讨论:若k≤0,则f′(x)>0,故f(x)在定义域上单调递增;
若k>0,令f′(x)>0,解得x>lnk;令f′(x)<0,解得x<lnk,
综上:当k≤0时,f(x)的单调递增区间为R,无单调递减区间;
当k>0时,f(x)的单调递增区间为(lnk,+∞),单调递减区间为(-∞,lnk),
(2)由题意:由(1)可知,当k≤0时,函数至多只有一个零点,不符合题意,舍去;
k>0时,令f(lnk)=elnk-klnk+k<0,解得k>e2,
此时f(1)=e>0;x→+∞时,f(x)→+∞>0,
因此会有两个零点,符合题意.
综上:实数k的取值范围是(e2,+∞).
点评 本题考查了函数的单调性问题,考查导数的应用以及函数恒成立问题,考查分类讨论思想,是一道综合题.

练习册系列答案
相关题目
17.在△ABC中,D是BC中点,E是AB中点,CE交AD于点F,若$\overrightarrow{EF}=λ\overrightarrow{AB}+u\overrightarrow{AC}$,则λ+u=( )
| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $-\frac{1}{3}$ | D. | 1 |
18.已知抛物线C:y2=4x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{FP}=5\overrightarrow{FQ}$,则|QF|=( )
| A. | $\frac{7}{2}$ | B. | $\frac{8}{5}$ | C. | $\frac{5}{2}$ | D. | 2 |
12.方程lnx+2x-6=0的近似解所在的区间是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
17.在等差数列{an}中,an>0,且a1+a2+…+a10=30,则a5+a6的值( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |