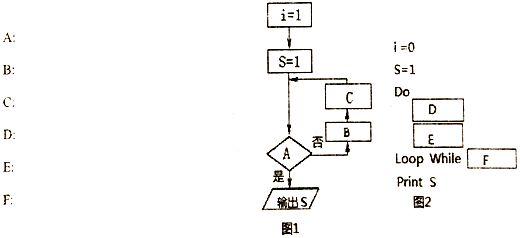
题目内容
12.方程lnx+2x-6=0的近似解所在的区间是( )| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
分析 根据单调性求解f(1)=-4,f(2)=ln2-2<0,f(3)=ln3>0,据函数的零点判断方法可得:零点在(2,3)内.
解答 解:令函数f(x)=lnx+2x-6,
可判断在(0,+∞)上单调递增,
∴f(1)=-4,f(2)=ln2-2<0,f(3)=ln3>0,
∴根据函数的零点判断方法可得:零点在(2,3)内,
方程lnx+2x-6=0的近似解:在(2,3)内.
故选:B
点评 本题考查了函数的零点,与方程的根的关系,根据函数的单调性判断分析,属于中档题.

练习册系列答案
相关题目
2.已知集合I,M,N的关系如图所示,则I,M,N的关系为( )
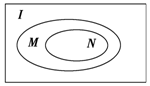

| A. | (∁IM)?(∁IN) | B. | M⊆(∁IN) | C. | (∁IM)⊆(∁IN) | D. | M?(∁IN) |
17.下列函数既是偶函数又是幂函数的是( )
| A. | y=x | B. | $y={x^{\frac{2}{3}}}$ | C. | $y={x^{\frac{1}{2}}}$ | D. | y=|x| |
4.已知f(x)是定义在R上的奇函数,对任意x>0,都有f(x+4)=f(x),若f(-2)=2,则f(2 018)等于( )
| A. | 2 012 | B. | 2 | C. | 2 013 | D. | -2 |